책 소개
요약
금융에 있어 반드시 관리해야 하는 위험 요소를 체계적으로 다루는 방법을 알려준다. 재무위험과 시장 위험, 신용 위험, 유동성 위험, 운영 위험 그리고 금융 붕괴를 예측하는 방법론을 차례로 설명하고 있으며, 이를 파이썬을 통해 실습할 수 있게 배려하고 있다.
1부는 금융 데이터에서 기본이 되는 시계열 데이터의 특성과 이를 처리하는 방법, 기본 개념을 설명한다. 시계열을 모델링할 수 있는 여러 기법을 자세하고 친절하게 소개한다. 2부에서는 본격적으로 위험 관리를 알아보는데, 위험을 ‘변동성’으로 정의한 해리 마코위츠부터 시작해서 시장 위험, 신용 위험, 유동성 위험, 운영 위험을 하나씩 살펴본다. 3부에서는 기업 지배 구조에 따른 주가 폭락의 위험을 감지하는 방법을 알아보고, 마지막으로 합성 데이터를 만드는 부분까지 소개한다.
추천의 글
”요즘 파이썬은 의심할 여지 없이 금융 분야 최고의 프로그래밍 언어다. 동시에 머신러닝은 이 산업 분야의 핵심 기술이 됐다. 압둘라 카라산이 쓴 이 책은 금융 위험 관리의 맥락에서 파이썬으로 머신러닝 능력을 훌륭하게 보여줬다. 이는 모든 금융기관에 필수적인 기능이다.”
—이브스 힐피시 박사(Dr. Yves J. Hilpisch)/
Python Quants and The AI Machine 설립자이자 CEO
“이 책은 재무 위험 분석을 위한 통계 및 머신러닝 전통에서 가져온 다양한 방법을 포괄적이고 실용적으로 제시한다. 재정 위험 분석에 통계와 머신러닝 방법을 적용하는 기법에 대한 가이드가 필요하다면 이 책을 추천한다.”
—그레이엄 길러(Graham L. Giller)/
『Adventures in Financial Data Science』 저자
“압둘라 카라산은 머신러닝의 현대적인 고급 애플리케이션을 적용해 금융 위험 관리라는 주제를 흥미진진하게 만들었다. 이 책은 계량 금융 경제학자, 헤지펀드 매니저 그리고 정량적 위험 관리 부서의 필수 도서다.”
—맥클레인 마샬(McKlayne Marshall)/
분석 참여 리더
이 책에서 다루는 내용
◆ 딥러닝 모델로 기존 시계열 애플리케이션을 검토, 비교
◆ 서포트 벡터 회귀, 신경망, 딥러닝을 사용한 위험도 측정을 위한 변동성 모델링 탐색
◆ 머신러닝 기술과 유동성 차원을 사용해 시장 위험 모델링(VaR 및 ES) 및 개선
◆ 군집화와 베이즈를 사용한 신용 위험 분석 개발 기법
◆ 가우스 혼합 모델과 코풀라 모델로 유동성 위험의 다양한 측면 포착
◆ 사기 탐지를 위한 머신러닝 모델 사용
◆ 머신러닝 모델을 사용해 주가 폭락을 예측하고 결정 요인을 식별
이 책의 대상 독자
모수적 모델에 크게 기반을 둔 현재의 금융 위험 관리 환경을 바꾸는 것을 목표로 하는 책이다. 머신러닝 모델을 기반으로 하는 매우 정확한 재무 모델이 최근 개발되면서 이러한 변화가 일어났다. 따라서 재무와 머신러닝에 대한 초기 지식이 있는 독자를 대상으로 하며, 이러한 주제를 간략하게 설명한다.
따라서 재무 위험 분석가, 재무 엔지니어, 위험 관련자, 위험 모델러, 모델 검증자, 정량적 위험 분석가, 포트폴리오 분석, 재무 그리고 데이터 과학에 관심이 있는 사람들이 읽기 적합하다.
이 책의 구성
1장, ‘리스크 관리의 기초’에서는 위험 관리의 주요 개념을 소개한다. 먼저 위험이 무엇인지 정의한 후 위험 유형(예: 시장, 신용, 운영 및 유동성)을 알아본다.
2장, ‘시계열 모델링 소개’에서는 이동 평균 모델, 자기 회귀 모델, 자기 회귀 통합 이동 평균 모델과 같은 기존 모델을 사용하는 시계열 애플리케이션을 보여준다.
3장, ‘시계열 모델링을 위한 딥러닝’에서는 시계열 모델링을 위한 딥러닝 도구를 소개한다.
4장, ‘머신러닝 기반 변동성 예측’에서는 서포트 벡터 회귀, 신경망, 딥러닝, 베이즈 접근 방식을 기반으로 하는 새로운 변동성 모델링을 다룬다. 성능 비교를 위해 기존의 ARCH, GARCH 유형의 모델도 사용한다.
5장, ‘시장 리스크 모델링’에서는 기존 시장 위험 모델, 즉 예상최대위험(VaR), 예상평균최대위험(ES)의 추정 성능을 높이는 데 사용되는 머신러닝 기반 모델에 대해 설명한다.
6장, ‘신용 위험 추정’에서는 신용 위험을 추정하는 포괄적인 머신러닝 기반 접근 방식을 소개한다.
7장, ‘유동성 모델링’에서는 가우스 혼합 모델을 사용해 위험 관리에서 간과되는 차원으로 여겨지는 유동성을 모델링한다.
8장, ‘운영 위험 모델링’에서는 회사의 내부 약점으로 인해 실패로 이어질 수 있는 운영 위험을 다룬다.
9장, ‘기업 지배 구조 리스크 측정: 주가 폭락’에서는 기업 지배 구조 위험을 모델링하는 완전히 새로운 접근 방식인 주가 폭락을 소개한다.
10장, ‘금융의 합성 데이터 생성과 은닉 마르코프 모델’에서는 다양한 재무 위험을 추정하기 위해 합성 데이터를 사용한다.
상세 이미지
목차
목차
- 1부. 위험 관리 기초
- 1장. 위험 관리의 기초
- 위험
- 수익률
- 위험 관리
- 주 재무 위험
- 금융 붕괴
- 금융 위험 관리에서의 정보 비대칭
- 역선택
- 도적적 해이
- 결론
- 참고문헌
- 2장 시계열 모델링 소개
- 시계열 구성 요소
- 추세
- 계절성
- 주기성
- 잔차
- 시계열 모델
- 백색 잡음
- 이동 평균 모형
- 자기회귀 모델
- 자기회귀 통합 이동 평균 모델
- 결론
- 참고문헌
- 3장. 딥러닝 시계열 모델링
- 순환신경망
- 장단기 기억
- 결론
- 참고문헌
- 2부. 시장, 신용, 유동성, 운영 리스크에서의 머신러닝
- 4장. 머신러닝 기반 변동성 예측
- ARCH 모델
- GARCH 모델
- GJR-GARCH
- EGARCH
- 서포트 벡터 회귀: GARCH
- 신경망
- 베이즈 접근 방법
- 마르코프 체인 몬테 카를로
- 메트로폴리스-헤이스팅스
- 결론
- 참고문헌
- 5장. 시장 위험 모델링
- 최대 예상 손실
- 분산- 공분산 기법
- 과거 시뮬레이션 방법
- 몬테 카를로 시뮬레이션 VaR
- 잡음 제거
- 최대 손실 평균
- 유동성 증대 ES
- 유효 비용
- 결론
- 참고문헌
- 6장. 신용 위험 추정
- 신용 위험 추정
- 위험 버켓팅
- 로지스틱 회귀를 사용한 채무불이행 추정
- 서포트 벡터 머신을 사용한 채무불이행 추정 확률
- 랜덤 포레스트를 사용한 채무불이행 추정 확률
- 신경망을 사용한 채무불이행 추정 확률
- 딥러닝을 사용한 채무불이행 추정 확률
- 결론
- 참고문헌
- 7장. 유동성 모델링
- 유동성 척도
- 거래량 기반 유동성 척도
- 거래 비용 기반 유동성 측정
- 코윈-슐츠 스프레드
- 가격 영향 기반 유동성 측정
- 시장 영향 기반 유동성 측정
- 가우스 혼합 모델
- 가우스 혼합 코풀라 모델
- 결론
- 참고문헌
- 8장. 운영 위험 모델링
- 사기 데이터에 익숙해지기
- 사기 조사를 위한 지도 학습
- 비용 기반 사기 조사
- 절약 점수
- 비용에 민감한 모델링
- 베이즈 최소 위험
- 사기 조사를 위한 비지도 학습 모델링
- 자기 구성맵
- 오토인코더
- 결론
- 참고문헌
- 3부. 기타 재무 위험 원인 모델링
- 9장. 기업 지배 구조 위험 측정: 주가 폭락
- 주가 폭락 측정
- 최소 공분산 행렬식
- 최소 공분산 행렬식의 적용
- 로지스틱 패널 응용
- 결론
- 참고문헌
- 10장. 금융의 합성 데이터 생성과 은닉 마르코프 모델
- 합성 데이터 생성
- 합성 데이터의 평가
- 합성 데이터 생성
- 은닉 마르코프 모델에 대한 간략한 소개
- 파마-프렌치 3요소 모델과 HMM 비교
- 결론
- 참고문헌
도서 오류 신고
정오표
정오표
[ p.56 : 9행 ]
즉 xt - xt-1을 의미하며
->
즉 xt - xt-1을 의미하며
[ p.119 : 12행 ]
그런 다음 σ2t-2를 ω+αr2t-3+βσ2t-3로 바꾼다.
->
그런 다음 σ2t-1를 ω+αr2t-2+βσ2t-2로 바꾼다.
[ p.126 : 1행 ]
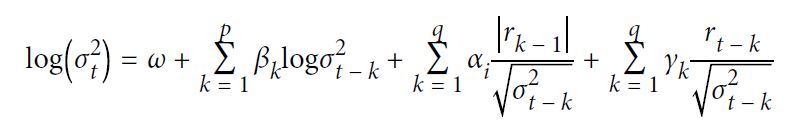
->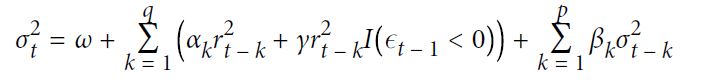
[ p.134 : 그림 4-7 ]
Volatility Prediction with EGARCH
->
Volatility Prediction with SVR-GARCH (Linear)
Volatility Prediction-EGARCH
->
Volatility Prediction-SVR-GARCH
[ p.170 : 코드 ]
def VaR_historical(initial_investment, conf_level):
Hist_percentile95 = []
for i, j in zip(stocks_returns.columns,
range(len(stocks_returns.columns))):
Hist_percentile95.append(np.percentile(stocks_returns.loc[:, i],
5))
print("Based on historical values 95% of {}'s return is {:.4f}"
.format(i, Hist_percentile95[j]))
VaR_historical = (initial_investment - initial_investment *
(1 + Hist_percentile95[j]))
print("Historical VaR result for {} is {:.2f} "
.format(i, VaR_historical))
print('--' * 35)
->
def VaR_historical(initial_investment, conf_level):
Hist_percentile95 = []
for i, j in zip(stocks_returns.columns,
range(len(stocks_returns.columns))):
Hist_percentile95.append(np.percentile(stocks_returns.loc[:, i],
5))
print("Based on historical values 95% of {}'s return is {:.4f}"
.format(i, Hist_percentile95[j]))
VaR_historical = (initial_investment - initial_investment *
(1 + Hist_percentile95[j]))
print("Historical VaR result for {} is {:.2f} "
.format(i, VaR_historical))
print('--' * 35)
[ p.173 : 4행 ]
원의둘레원/면적사각형
->
면적원/면적사각형
[ p.173 : 6행 ]
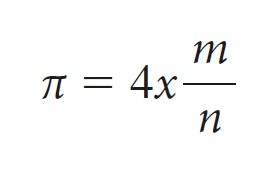
->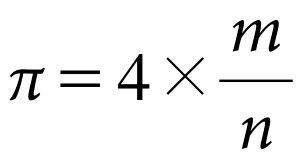
[ p.243 : 11행, 12행 ]
7장
->
6장