그래프 머신러닝 [머신러닝 알고리듬을 적용해 그래프 데이터 활용하기]
- 원서명Graph Machine Learning: Take graph data to the next level by applying machine learning techniques and algorithms (ISBN 9781800204492)
- 지은이클라우디오 스타밀레(Claudio Stamile), 알도 마르줄로(Aldo Marzullo), 엔리코 듀세비오(Enrico Deusebio)
- 옮긴이김기성, 장기식
- ISBN : 9791161757209
- 35,000원 (eBook 28,000원)
- 2023년 01월 31일 펴냄
- 페이퍼백 | 360쪽 | 188*235mm
- 시리즈 : 데이터 과학
책 소개
소스 코드 파일은 여기에서 내려 받으실 수 있습니다.
한국어판의 코드는 여기에서 내려 받으실 수 있습니다.
요약
파이썬으로 그래프 데이터를 다루기 위한 패키지인 NetworkX는 손쉽게 그래프를 생성, 조작, 분석하기 위한 매우 유용한 도구이다. NetworkX로 그래프 데이터를 이해하기 위한 기본적인 방법과 더불어 node2vec, edge2vec과 같은 다양한 머신러닝 알고리듬을 이용해 그래프 데이터를 활용하는 방법을 실생활에 적용가능한 예시와 함께 소개한다.
이 책에서 다루는 내용
◆ 그래프 특징을 추출하는 파이썬 스크립트 작성법
◆ 주요 비지도 및 지도 그래프 임베딩 기술 구현 방법
◆ 주요 그래프 표현 학습 기법의 차이점
◆ 얕은 임베딩 방법, 그래프 신경망, 그래프 정칙화 방법 등
◆ 소셜 네트워크 및 금융 거래 시스템 등에서의 데이터 추출 방법
◆ 애플리케이션을 원활하게 배포하고 확장하는 방법
이 책의 대상 독자
이 책은 데이터 포인트를 풀고, 위상(topology) 정보를 활용해 분석과 모델의 성능을 개선하려는 데이터 분석가, 그래프 개발자, 그래프 분석가, 그래프 전문가를 대상으로 한다. 머신러닝 기반 그래프 데이터베이스를 구축하려는 데이터 과학자와 머신러닝 개발자에게도 유용하다. 그래프 데이터베이스와 그래프 데이터에 대한 초급 수준의 지식을 가지고 있는 사람이 읽기에 적합한 책이다. 이 책의 내용을 최대한 활용하기 위해서는 파이썬 프로그래밍과 머신러닝에 대한 중급 수준의 실무 지식 또한 필요하다.
이 책의 구성
1장, '그래프 시작하기’에서는 NetworkX 파이썬 라이브러리를 사용해 그래프 이론의 기본 개념을 소개한다.
2장, ‘그래프 머신러닝’에서는 그래프 머신러닝과 그래프 임베딩 기술의 주요 개념을 소개한다.
3장, ‘그래프 비지도 학습’에서는 비지도 그래프 임베딩의 최신 방법을 다룬다.
4장, ‘그래프 지도 학습’에서는 지도 그래프 임베딩의 최신 방법을 다룬다.
5장, ‘그래프에서의 머신러닝 문제’에서는 그래프에서 가장 일반적인 머신러닝 작업을 소개한다.
6장, ‘소셜 네트워크 그래프’에서는 분석 소셜 네트워크 데이터에 머신러닝 알고리듬을 적용하는 방법을 소개한다.
7장, ‘그래프를 사용한 텍스트 분석 및 자연어 처리’에서는 자연어 처리 작업에 머신러닝 알고리듬을 적용하는 방법을 소개한다.
8장, ‘신용카드 거래에 대한 그래프 분석’에서는 신용카드 부정 거래 탐지에 머신러닝 알고리듬을 적용하는 방법을 소개한다.
9장, ‘데이터 드리븐 그래프 기반 응용 프로그램 구축’에서는 큰 그래프를 처리하는 데 유용한 몇 가지 기술을 소개한다.
10장, ‘그래프의 새로운 트랜드’에서는 그래프 머신러닝의 몇 가지 새로운 동향(알고리듬과 응용 프로그램)을 소개한다.

목차
목차
- 1부. 그래프 머신러닝 소개
- 1장. 그래프 시작하기
- 기술적 필요 사항
- networkx로 그래프 이해하기
- 그래프의 종류
- 그래프 표현
- 그래프 플로팅
- networkx
- Gephi
- 그래프 속성
- 통합 측정 지표
- 분리 측정 지표
- 중심성 측정 지표
- 탄력성 측정 지표
- 벤치마크 및 저장소
- 간단한 그래프의 예
- 그래프 생성 모델
- 벤치마크
- 큰 그래프 다루기
- 요약
- 2장. 그래프 머신러닝
- 기술적 필요 사항
- 그래프 머신러닝 이해하기
- 머신러닝의 기본 원리
- 그래프 머신러닝의 이점
- 일반화된 그래프 임베딩 문제
- 그래프 임베딩 머신러닝 알고리듬의 분류
- 임베딩 알고리듬의 분류
- 요약
- 2부. 그래프에서의 머신러닝
- 3장. 비지도 그래프 학습
- 기술적 필요 사항
- 비지도 그래프 임베딩 로드맵
- 얕은 임베딩 방법
- 행렬 분해
- 그래프 분해
- 고차 근접 보존 임베딩
- 전역 구조 정보를 통한 그래프 표현
- skip-gram
- DeepWalk
- Node2Vec
- Edge2Vec
- Graph2Vec
- 오토인코더
- 텐서플로와 케라스-강력한 조합
- 첫 번째 오토인코더
- 노이즈 제거 오토인코더
- 그래프 오토인코더
- 그래프 신경망
- GNN의 변형
- 스펙트럼 그래프 합성곱
- 공간 그래프 합성곱
- 예제로 보는 그래프 합성곱
- 요약
- 4장. 지도 그래프 학습
- 기술적 필요 사항
- 지도 그래프 임베딩 로드맵
- 특징 기반 방법
- 얕은 임베딩 방법
- 라벨 전파 알고리듬
- 라벨 확산 알고리듬
- 그래프 정규화 방법
- 매니폴드 정규화 및 준지도 임베딩
- 신경 그래프 학습
- Planetoid
- Graph CNN
- GCN을 이용한 그래프 분류
- GraphSAGE를 이용한 노드 분류
- 요약
- 5장. 그래프에서의 머신러닝 문제
- 기술적 필요 사항
- 그래프에서 누락된 링크 예측
- 유사성 기반 방법
- 임베딩 기반 방법
- 커뮤니티와 같은 의미 있는 구조 감지
- 임베딩 기반 커뮤니티 감지
- 스펙트럼 방법 및 행렬 분해
- 확률 모델
- 비용 함수 최소화
- 그래프 유사성 및 그래프 매칭 감지
- 그래프 임베딩 기반 방법
- 그래프 커널 기반 방법
- GNN 기반 방법
- 응용
- 요약
- 3부. 그래프 머신러닝의 고급 응용
- 6장. 소셜 네트워크 그래프
- 기술적 필요 사항
- 데이터셋 개요
- 데이터셋 다운로드
- networkx로 데이터셋 불러오기
- 네트워크 토폴로지 및 커뮤니티 감지
- 토폴로지 개요
- 노드 중심성
- 커뮤니티 감지
- 지도 및 비지도 임베딩
- 작업 준비
- node2vec 기반 링크 예측
- GraphSAGE 기반 링크 예측
- 링크 예측을 위한 수작업 특징
- 결과 요약
- 요약
- 7장. 그래프를 이용한 텍스트 분석 및 자연어 처리
- 기술적 필요 사항
- 데이터셋 개요
- 자연어 처리에서 사용되는 주요 개념 및 도구 이해
- 문서 모음에서 그래프 만들기
- 지식 그래프
- 이분 문서/개체 그래프
- 문서 주제 분류기 구축
- 얕은 학습 방법
- 그래프 신경망
- 요약
- 8장. 신용카드 거래에 대한 그래프 분석
- 기술적 필요 사항
- 데이터셋 개요
- 데이터셋 불러오기 및 networkx 그래프 구축
- 네트워크 토폴로지 및 커뮤니티 감지
- 네트워크 토폴로지
- 커뮤니티 감지
- 사기 탐지를 위한 지도 및 비지도 임베딩
- 사기 거래 식별에 대한 지도 학습 접근 방식
- 사기 거래 식별에 대한 비지도 학습 접근 방식
- 요약
- 9장. 데이터 드리븐 그래프 기반 응용 프로그램 구축
- 기술적 필요 사항
- 람다 아키텍처 개요
- 그래프 기반 응용 프로그램을 위한 람다 아키텍처
- 그래프 처리 엔진
- 그래프 쿼리 레이어
- Neo4j와 GraphX 선택
- 요약
- 10장. 그래프의 새로운 트렌드
- 그래프의 데이터 증대에 대해 알아보기
- 샘플링 전략
- 데이터 증강 기술 살펴보기
- 토폴로지 데이터 분석에 대해 배우기
- 토폴로지 머신러닝
- 새로운 영역에 그래프 이론 적용하기
- 그래프 머신러닝 및 신경 과학
- 그래프 이론 및 화학 및 생물학
- 그래프 머신러닝 및 컴퓨터 비전
- 추천 시스템
- 그래프의 데이터 증대에 대해 알아보기
도서 오류 신고
정오표
정오표
[ 본문 전체 ]
대역효율성
->
전역효율성
[ p.54 : 수식 ]
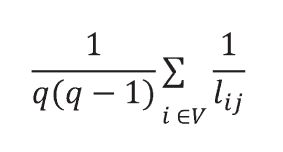
->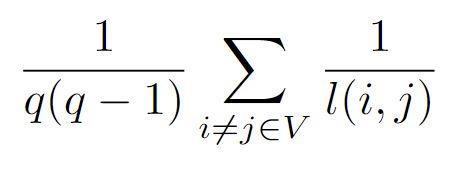
[ p.54 : 5행 ]
노드의 대역효율성은 노드의 근방만 고려해 계산할 수 있다. 대역효율성은 다음의 코드와 같이 networkx를 사용해 계산할 수 있다.
->
노드의 국소효율성(local efficiency)은 노드 자체는 계산에 포함하지 않고 인접 노드만 고려해 계산할 수 있다. 전역효율성은 다음의 코드와 같이 networkx를 사용해 계산할 수 있다.
[ p.64 : 5행 ]
바벨그래프는 크기가 m1과 m2인 2개의 클리크가 노드 가지로 연결된 그래프로,
->
바벨그래프는 크기가 m1과 m2인 2개의 클리크가 노드 가지로 연결된 그래프로,
[ p.75 : 7행 ]
노드가나 간선의 개수를 늘릴 때
->
노드나 간선의 개수를 늘릴 때
[ p.81 : 8행 ]
미첼(Mitchell, 1997)은 작업 T에 대해 측정한 성능 P가 경험 E를 향상시킬 때 알고리듬은 경험 E로부터 학습한다고 정의했다.
->
미첼(Mitchell, 1997)은 경험 E로부터 성능 P를 사용해 작업 T의 성능이 향상되면 알고리듬은 경험 E로부터 학습한다고 정의했다.
[ p.104 : 아래에서 4행 ]
W ∈ ℝm × d
->
V ∈ ℝm × d
[ p.128 : 두번째 코드 1행 ]
n = 10
->
n = 6
[ p.130 : 그림 3.15 ]
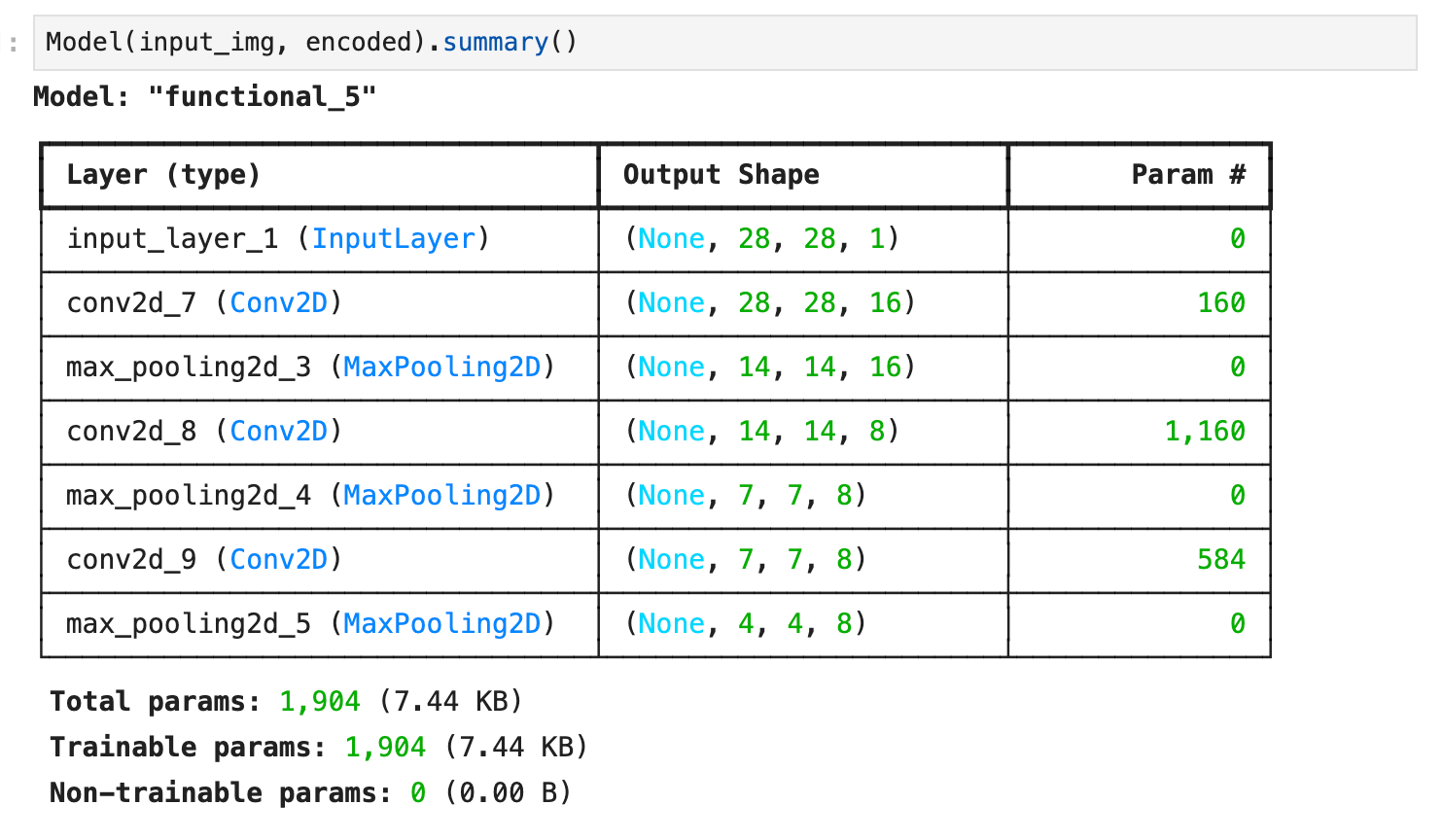
[ p.134 : 2행 ]
데이터셋이 더 작을 때 네트워크가 노이즈를 ‘학습’하지 않도록 하는 대안(따라서 정적 노이즈 이미지와 노이즈 없는 버전 간의 매핑을 학습)은 GaussianNoise 레이어를 사용해 학습 중에 확률적 노이즈를 추가하는 것이다.
->
데이터셋이 작은 경우, 네트워크가 노이즈 자체도 '학습'하는 (따라서 정적 노이즈 이미지와 노이즈 없는 버전 간의 매핑을 학습하는) 것을 방지하는 대안은 GaussianNoise 레이어를 사용해 학습 중에 확률적 노이즈를 추가하는 것이다.
[ p.136 : 아래에서 2행 ]
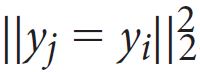
->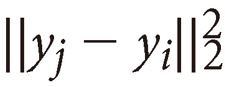
[ p.137 : 수식 ]
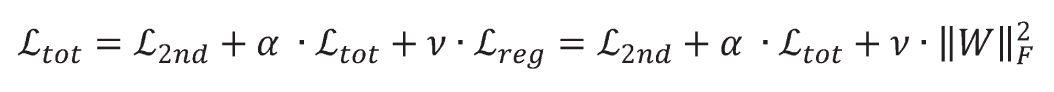
->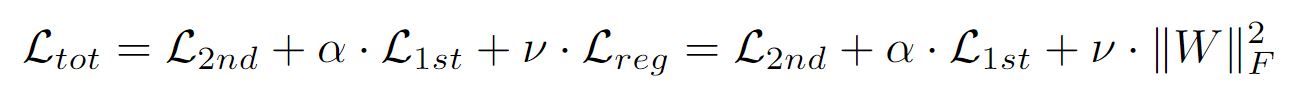
[ p.160 : 첫번째 코드 4행부터 ]
c_tool = 10
while it < self.max_iter & c_tool > self.tol:
Y = A*Y_prev
# 라벨 강제 할당
Y[labeled_index] = Y0[labeled_index]
it +=1
c_tol = np.sum(np.abs(Y-Y_prev))
Y_prev = Y
->
c_tool = 10
while it < self.max_iter and c_tool > self.tol:
Y = np.dot(A, Y_prev)
#force labeled nodes
Y[labeled_index] = Y0[labeled_index]
it +=1
c_tol = np.sum(np.abs(Y-Y_prev))
Y_prev = Y
[ p.163 : 코드 아래에서 5행 ~ p. 164 : 코드 ]
Y_prev = Y0
it = 0
c_tool = 10
while it < self.max_iter & c_tool > self.tol:
Y = (self.alpha*(L*Y_prev))+((1-self.alpha)*Y0)
it +=1
c_tol = np.sum(np.abs(Y-Y_prev))
&Y_prev = Y
&self.label_distributions_ = Y
&return self
->
Y_prev = Y0
it = 0
c_tool = 10
while it < self.max_iter & c_tool > self.tol:
Y = self.alpha*(L*Y_prev)+((1-self.alpha)*Y0)
it +=1
c_tol = np.sum(np.abs(Y-Y_prev))
Y_prev = Y
self.label_distributions_ = Y
return self