Top

The R Book (Second Edition) 한국어판 [R로 배우는 데이터 분석 기술]

  • 원서명The R Book (ISBN 9780470973929)
  • 지은이마이클 크롤리(Michael J. Crawley)
  • 옮긴이정사범, 권정민
  • ISBN : 9788960775435
  • 55,000원
  • 2014년 03월 31일 펴냄 (절판)
  • 페이퍼백 | 1,154쪽 | 188*250mm
  • 시리즈 : 데이터 과학

판매처

  • 현재 이 도서는 구매할 수 없습니다.
파일다운로드

책 소개

책 표지 이미지 아래의 [파일 다운로드] 버튼을 통해 내려받으실 수 있는 부속 데이터 파일은 원저자가 제공한 데이터 파일입니다. 본문에서 설명하는 예제 중 일부 데이터 파일은 제공되지 않습니다.

요약

빅데이터 시대에 가장 범용적으로 사용되는 통계 언어인 R의 기초부터 활용까지 전반적인 내용과 상세한 예제를 다룬 책이다. 이 책에서는 R을 이용하여 데이터 처리에 필요한 기초문법과 그래픽부터 가설 검정, 회귀분석, 분산 분석, 다변량 분석, 시계열 분석, 생존 분석, 베이지안 통계 등의 고급 분석까지 폭 넓게 다루고 있다. 이 책 한 권으로 R언어 초보자부터 전문가까지 누구나 필요로 하는 데이터 처리와 분석에 대한 다양한 정보를 습득할 수 있다. 특히 각 주제에 대한 분석방법을 상세한 예제코드와 함께 소개하고 있어 데이터 분석 기술과 R 프로그래밍 기술을 쉽게 익히고 실행하여 볼 수 있다.

이 책에서 다루는 내용

■ 필요한 정보를 효율적으로 찾을 수 있도록 명확한 구조로 설명
■ 지난 5년 동안 R의 변화 과정 한눈에 살펴보기
■ 베이지안 분석과 메타 분석에 대한 설명
■ 참고문헌과 참고자료 부록 수정과 업데이트
■ 책 내용에 있는 예제를 사용자가 실행해볼 수 있는 예제 코드 제공

이 책의 대상 독자

■ 컴퓨터와 통계 초보자
■ 프로젝트 작업에 도움이 필요한 학생
■ R과 통계 작업을 수행한 경험이 있으나 두 분야에 대해 배우고 싶은 사람
■ 회귀 분석과 분산 분석 경험이 있으나 고급 통계 모델링을 배우고 싶은 사람
■ 통계 경험이 있는 R 초보자
■ 컴퓨터 경험이 있는 R 초보자
■ 통계와 컴퓨터에 익숙하지만 참고서가 필요한 사람

추천의 글

“여러분이 R 사용자이거나 사용자가 되고 싶다면, 이 책은 항상 여러분 곁에 두고 참고해야 하는 책이다. R 언어로 데이터를 분석하는 방법에 대한 수많은 도서 중에서 단연 돋보이는 책이다.” - 미국 통계학자

“높은 수준의 소프트웨어인 R 언어는 정량 분석의 표준을 만들어 가고 있다. 이 책 덕분에 누구든지 R 언어에 대해 이해할 수 있게 되었다.” - 연금기관 데이터 분석전문가

“이 책은 R 환경에 대한 도서에서 중요한 위치를 차지하고 있으며, R을 사용한 통계 분석 방법에 대한 전문지식을 다룬다. 과학에서 경제학, 그리고 의학에서 공학에 이르기까지 다양한 분야에서 R을 활용한 통계 분석 기술을 배우려고 하는 초보 및 중급 사용자를 대상으로 한다.” -컴퓨팅 리뷰

“완벽하게 개정되고 업데이트된 참고문헌과 참고자료 섹션을 제공한다. 또한 사용자가 실행해 볼 수 있도록 본문에 실린 예제를 웹 사이트에서 지원한다.” -Zentralbalt Math

“전반적으로 이 책은 막강하고 지속적으로 진화하고 있는 R 언어에 대한 좋은 가이드다. 완전한 레퍼런스에 가깝고, 다루는 내용은 매우 다양하며 우수하다. R에 대한 가이드인 이 책을 통해 좀 더 쉽게 R을 사용할 수 있을 것이다.” -Nekkidblogger.com

“이 책은 학기 중에 학생들에게 판매하는 교재보다 훨씬 더 큰 매력을 갖고 있는 고전이다. 이 책은 출간되면 베스트셀러가 될 것이다.” -북셀러

저자/역자 소개

저자 서문

R은 데이터 분석과 그래픽을 위한 고급 프로그래밍 언어이자 환경이다. R은 베커(Becker), 챔버(Chambers), 윌크스(Wilks)의 S 언어와 수스만(Sussman)의 스킴(Scheme) 언어에 영향을 받았다. R 언어는 S 언어와 매우 비슷하지만 기본 구현과 의미는 스킴 언어에서 파생되었다. 이 책은 과학에서 경제학, 그리고 의학에서 공학에 이르기까지 다양한 분야의 초보와 중급 사용자를 대상으로 R 환경을 소개하는 것을 목적으로 한다. 이 책이 R에 대한 교과서뿐만 아니라 참고서로도 사용될 수 있기를 바란다.

책의 전반부는 통계나 컴퓨터에 대한 배경 지식이 없는 독자들을 대상으로 설명했지만, 후반부는 전반부에 대한 지식이 있다는 가정하에 설명했다. 이 책은 데이터 처리, 그래픽, 수학 함수, 광범위한 통계 분석 방법을 다룬다. 통계 분석 방법으로는 회귀 분석, 분산 분석, 일반화 선형모델링과 같은 기초 분석에서 시작하여 베이지안 분석, 공간 통계, 다변량 분석, 의사결정나무 모델, 혼합효과 모델, 시계열 분석 등과 같은 전문적인 주제를 다룬다. 검정 분석 이면에 깔린 가정을 설명하고, 통계 모델링에 중요한 접근 방법을 설명하지만, 통계 이론을 거의 포함하지 않았고 수학이나 통계 관련 배경 지식이 없어도 이해할 수 있게 했다.

여러분은 이미 적합한 통계 패키지를 숙달했을 텐데, 굳이 R 언어로 전환하려고 하는가? 이미 능숙한 통계 패키지가 있고, 매우 제한된 범위의 통계 검정을 수행하고 향후에 많거나 다양한 분석 작업을 수행하지 않는다면 굳이 전환할 필요가 없다. R 언어로 전환해야 하는 주요 이유는 첫째, 타의 추종을 불허하는 다양한 분야의 분석 사례와 둘째, 혼합효과 모델링이나 일반화 가법 모델링과 같은 새로운 최첨단 애플리케이션을 사용할 수 있기 때문이다. R을 학습해야 하는 두 번째 이유는 논문을 포함한 통계 관련 문서를 이해하기 위해서다. 더 많은 사람들이 R의 맥락에서 분석 결과 보고서를 작성하고 있으며, 보고서 작성자가 무엇에 대해 말하고 있는지에 대해 아는 것이 중요하다.

R을 사용하는 다른 분석가를 알아보기 위해 주위를 둘러보자. 많은 사람이 이미 R로 전환했다. 세계 최고의 통계학자들 또한 대부분 R을 사용하고 있으며 이러한 사실은 많은 사람들이 R에 기여하고 있다는 것을 말해준다. R로 변경해야 하는 세 번째 이유는 고품질의 유용한 후원과 지원이 있기 때문이다. 웹상에는 R에 대한 질문에 답해줄 수 있는 전용 R 마법사라는 훌륭한 네트워크가 있다. 통계 계산을 잘하기 위해 노력하려 한다면, R의 구조와 이를 이용해 함수를 작성할 수 있다는 점은 큰 도움이 된다. 마지막으로, 이 제품은 무료라는 점이다. R은 세상에서 가장 훌륭한 통합 소프트웨어이며, 무료로 제공되기까지 한다.

대부분의 명령 코드는 S-PLUS에서도 똑같이 사용되지만, 일부분은 상당한 차이가 있다. 따라서 혼동하지 않도록 주로 R을 설명하는 데 집중했다. 어느 부분에서 S-PLUS가 R과 다른지는 설명하지는 않았다. 그러므로 S-PLUS에서 작업해야 한다면, 실제로 문제없이 실행되는지 확인해보는 것이 좋다

저자 소개

마이클 크롤리 (Michael Crawley)

영국 런던 임페리얼 칼리지 실우드파크 캠퍼스에서 강의하고 계신 교수다. 영국왕립학회 회원(Fellow of the Royal Society)이며 R과 통계학 관련 베스트셀러인 『Statistics: An Introduction using R』과 『Statistical Computing: An Introduction to Data Analysis Using S-Plus』의 저자이기도 하다.

옮긴이의 말

흔히들 빅 데이터를 디지털 원유라고 부르며 이를 분석하면 막강한 정보력을 갖출 수 있다고들 합니다. 최근 몇 년 동안 빅 데이터는 IT 분야에서 큰 이슈가 되고 있으며 이러한 움직임은 한국에서도 화두가 되었습니다. 이러한 현상은 다양한 컨퍼런스와 세미나, 학회, 온/오프모임이 생기는 것만 봐도 알 수 있습니다. 정부와 기업에서는 빅 데이터 관련 R&D, 인력 양성, 관련 조직을 구성하고 있으며 일부 프로젝트에서는 의미 있는 결과물을 만들어내고 있습니다. 이로 인해 최근 들어 서비스나 제조업 관련 기업에서 관심을 갖기 시작하고 있는 분야라고 할 수 있습니다.

유럽과 미국을 위주로 해 10여 년 전부터 데이터 분석 영역은 다양한 학회와 연구 활동이 있었고, 이를 기반으로 데이터 분석 전문인력 양성을 위한 다양한 과정이 운영되어 왔습니다. 최근 들어 국내에도 데이터 분석 전문인력을 양성하기 위해 대학에서도 다양한 과정이 생기고 있는데, 이는 상당히 고무적인 일입니다. 또한 온/오프 형태로 현업 종사자들이 모여서 R 언어를 포함한 빅 데이터 정보를 공유하고 있습니다.

데이터를 분석하는 데 반드시 필요한 것은 해당 영역에 대한 지식, 분석 툴, 분석 방법이라고 할 수 있습니다. 3가지 요소 중에 R 언어는 분석을 위한 대표적인 툴 중의 하나입니다. 따라서 전문인력 양성 과정에는 데이터 분석 툴과 분석 방법이 반드시 포함되어 있어야 할 것입니다.
해외는 물론 국내에 다양한 온오프 모임과 교육 과정이 개설되었으며 관심을 갖는다면 해당 과정을 등록해 수강할 수 있습니다. 조금만 관심을 갖는다면 이 책을 포함해 데이터 분석 방법을 배울 수 있는 기회는 다양하며, 손쉽게 찾아볼 수 있습니다.

현업에 계신 분들은 아시겠지만 데이터 분석은 혼자서 하는 작업이 아닙니다. 데이터 분석 결과에 의미가 있으려면 반드시 분석 대상이 되는 분야에 대해 깊이 이해해야 합니다. 이러한 기반하에서 관련 데이터를 모으고 프로그래밍 기술과 데이터 분석 기술, 통찰력을 발휘하여 의미 있는 결과를 만들어내는 것입니다. 따라서 데이터 분석을 제대로 하려면 다양한 분야에 대한 이해와 지식을 바탕으로 해 데이터 분석 방법을 만들어 내고 툴을 사용해 데이터를 분석해야 합니다.

이러한 측면에서 분석 방법과 분석 툴 분야에 대한 분석가의 역량 개발에 있어 이 책은 좋은 참고 도서가 될 수 있습니다. 기존의 다른 책과는 달리 R의 사용법부터 시작해 실제 업무에 필요한 다양한 통계 분석 방법을 R 언어로 분석하는 과정을 상세하게 보여줍니다.

이 책은 초판이 출간된 이후 2012년에 베이지안 분석과 메타 분석이 추가되어 개정 출간된 버전을 번역한 책입니다. 원서가 R 언어와 분석 방법을 다양하게 다루다 보니 1,000페이지가 넘는 상당히 많은 분량이었으며 번역하는 데에도 상당한 시간이 소요되었습니다.
정사범

R을 업무에서 본격적으로 사용하게 된 지도 벌써 4-5년이 되었다. 처음에 학교에서 S-PLUS나 R을 접하면서도 SAS나 SPSS 같이 편리한 것도 아니며 눈에 띄게 다른 점도 없어서 그냥 좀 주변에서 사용되다가 사장될 줄 알았는데, 예상과 달리 이 언어를 주 업무로 사용하고, 책을 번역하게 될 것이라고는 전혀 생각하지 못했다.

하지만, 빅 데이터가 화두가 되면서 데이터 분석에 대한 관심이 높아지고 사용 형태가 좀 더 다변화되면서, 데이터 분석 분야에서 이런 경험과 방법을 공유하고 사회와 기술의 변화에 발 맞춰 가는 데 현재로서는 R만큼 적합한 도구는 없다고 생각된다. 이런 의미에서 이 책을 번역하게 되어서 매우 기쁘게 생각한다.

이 책은 R을 사용하고 공부하고자 하는 사람이면 초보자건, 전문가건 누구에게나 도움이 될 수 있는 내용들이 실려 있는 일종의 R 바이블이라고 해도 과언이 아니다. 기본적인 R의 개념과 문법으로 시작해서 베이지안 분석론이나 생존 분석 등에 대한 고급 분석에 대한 내용까지 풍부한 예제와 함께 상세하게 기술되어 있다. 나도 R을 어느 정도 사용해봤지만, 이 책을 번역하면서 이론으로만 알던 내용이 R로 구현된 것을 처음 접해보는 등 새로운 내용을 접할 수 있었다. 쉽지 않은 작업인 데다가 상당히 긴 분량을 번역하면서 지루해질 법도 한데, 그런 이유에서인지 굉장히 재미있고 흥미로운 시간을 보낼 수 있었다. 이 책을 읽는 독자 분들도 이 책이 주는 광대한 지식과 더불어 이런 감정 역시 공유할 수 있었으면 한다.
권정민

옮긴이 소개

정사범

대학에서 산업공학을 전공하면서 의사결정 최적화 방법론에 대해 관심이 많았다. 2000년이 시작될 즈음 입사한 이후 지금까지 제품을 기획하고 만들어내는 과정에서 발생되는 다양한 데이터를 분석해왔다. 지금도 다양한 분야에서 데이터 분석 관련 프로젝트를 수행하고 있으며, 해당 분야의 업무에 조금이라도 도움이 될 만한 가치를 만들어 내려고 고민하고 있다. 최근에는 제품을 개발하고 생산하는 과정에서 다양한 데이터 분석방법을 활용하여 Smart Manufacturing을 현실화할 수 있는 방법에 대해 알고자 열심히 노력 중이다. 에이콘출판사에서 출간한 『RStudio 따라잡기』(2013), 『예측 분석 모델링 실무 기법』(2014)을 번역했다.

권정민

세상은 데이터로 이루어져 있다고 생각하며, 이를 잘 활용해 좀 더 많은 사람을 널리 즐겁게 하자는 목표를 가지고 다양한 데이터 분석 및 활용 방안을 고민하고 연구하는 것을 업으로 하고 있다. 카이스트와 포스텍에서 산업공학과 전산학을 전공했으며 다양한 산업군에서 데이터 분석을 해왔다. 데이터가 화두로 떠오르기 조금 전에 세상이 데이터로 이뤄졌음을 깨달았다는 것에 조그마한 자부심을 느끼며, 데이터에서 가치를 찾아내는 일을 좀 더 즐겁고 지속적으로 할 수 있는 방안을 찾고자 매일 고민하며 연구한다. 『빅데이터 분석 도구 R 프로그래밍』(에이콘출판, 2012),『파이썬을 활용한 베이지안 통계』 등을 번역했다.

목차

목차
  • 1장 시작
    • 1.1 이 책의 사용법
      • 1.1.1 컴퓨터와 통계 초보자
      • 1.1.2 프로젝트 작업에 도움이 필요한 학생
      • 1.1.3 R과 통계 작업을 수행한 경험이 있으나 좀 더 배우고 싶은 사람
      • 1.1.4 회귀 분석과 분산 분석 경험이 있으나 고급 통계 모델링을 배우고 싶은 사람
      • 1.1.5 통계 경험이 있는 R 초보자
      • 1.1.6 컴퓨터 경험이 있는 R 초보자
      • 1.1.7 통계와 컴퓨터에 익숙하지만 참고서가 필요한 사람
    • 1.2 R 설치
    • 1.3 R 실행
    • 1.4 포괄적 R 아카이브 네트워크
      • 1.4.1 매뉴얼
      • 1.4.2 자주 묻는 질문
      • 1.4.3 기증 문서
    • 1.5 R에서 도움말 사용
      • 1.5.1 함수 예제
      • 1.5.2 R 함수에 대한 데모
    • 1.6 R 패키지
      • 1.6.1 패키지의 내용
      • 1.6.2 패키지 설치
    • 1.7 명령 행 vs. 스크립트
    • 1.8 데이터 편집기
    • 1.9 R 화면의 모양 변경
    • 1.10 실행 후 정리
    • 1.11 다른 컴퓨터 언어와 연계
  • 2장 R 언어의 기초
    • 2.1 계산
      • 2.1.1 복소수
      • 2.1.2 반올림
      • 2.1.3 산술
      • 2.1.4 나머지와 몫
      • 2.1.5 변수명과 할당
      • 2.1.6 연산자
      • 2.1.7 정수
      • 2.1.8 요인
    • 2.2 논리연산자
      • 2.2.1 TRUE와 T, FALSE와 F
      • 2.2.2 실수값에 대한 동등 여부 테스트
      • 2.2.3 all.equal을 사용한 부동 소수점 숫자의 동등 여부 확인
      • 2.2.4 all.equal 함수를 사용한 개체 간 차이 요약
      • 2.2.5 참과 거짓의 조합에 대한 연산
      • 2.2.6 논리연산
    • 2.3 수열 생성
      • 2.3.1 반복 생성
      • 2.3.2 요인 수준 생성
    • 2.4 멤버십: R에서 테스팅과 강제 형변환
    • 2.5 결측값, 무한대, 숫자가 아닌 값
      • 2.5.1 결측값: NA
    • 2.6 벡터와 첨자
      • 2.6.1 첨자를 사용해 벡터 요소 추출
      • 2.6.2 벡터 클래스
      • 2.6.3 벡터에서 요소 명명
      • 2.6.4 논리 첨자로 분석
    • 2.7 벡터 함수
      • 2.7.1 tapply 함수로 평균 테이블 계산
      • 2.7.2 그룹 요약 통계를 위한 집계 함수
      • 2.7.3 P병렬 최솟값과 최댓값: pmin과 pmax
      • 2.7.4 그룹별 벡터 요약 정보
      • 2.7.5 벡터 내에서 주소
      • 2.7.6 가장 가까운 값 검색
      • 2.7.7 정렬, 순위, 순서
      • 2.7.8 unique와 duplicated의 차이 이해
      • 2.7.9 벡터에서 실행 횟수 산출
      • 2.7.10 집합: union, intersect, setdiff
    • 2.8 행렬과 배열
      • 2.8.1 행렬
      • 2.8.2 행렬의 행과 열에 이름 지정
      • 2.8.3 행렬의 행 또는 열 계산
      • 2.8.4 행렬에 행과 열 추가
      • 2.8.5 sweep 함수
      • 2.8.6 apply, sapply, lapply로 함수 적용
      • 2.8.7 max.col 함수 사용
      • 2.8.8 aperm을 이용한 다차원 배열의 구조 조정
    • 2.9 임의의 숫자, 샘플링과 셔플링
      • 2.9.1 샘플링 함수
    • 2.10 루프와 반복
      • 2.10.1 이진 변환
      • 2.10.2 루프 방지
      • 2.10.3 루프 속도 저하
      • 2.10.4 연결 또는 재귀 함수를 호출해 데이터 집합을 증가시키지 말 것
      • 2.10.5 시계열 생성을 위한 루프
    • 2.11 리스트
      • 2.11.1 리스트와 lapply
      • 2.11.2 리스트 조정과 저장
    • 2.12 텍스트와 문자열, 패턴 일치
      • 2.12.1 문자열 연결
      • 2.12.2 부분 문자열 추출
      • 2.12.3 문자열 내에 대상 문자의 개수 계산
      • 2.12.4 대문자와 소문자
      • 2.12.5 match 함수와 관계형 데이터 베이스
      • 2.12.6 패턴 매칭
      • 2.12.7 모든 것이라는 의미의 점 문자
      • 2.12.8 문자열 내에서 텍스트 교체
      • 2.12.9 regexpr을 사용해 벡터 내에서 패턴 위치 검색
      • 2.12.10 %in%와 which 사용
      • 2.12.11 패턴 일치 심화
      • 2.12.12 Perl 정규표현식
      • 2.12.13 복잡한 문자열에서 패턴화된 텍스트 제거
    • 2.13 R에서 날짜와 시간
      • 2.13.1 파일에서 시간 데이터 인식
      • 2.13.2 strptime 함수
      • 2.13.3 difftime 함수
      • 2.13.4 날짜와 시간 계산
      • 2.13.5 difftime과 as.difftime 함수
      • 2.13.6 날짜 배열 생성
      • 2.13.7 데이터 프레임의 행 간 시간 차이 계산
      • 2.13.8 날짜와 시간을 이용한 회귀분석
      • 2.13.9 R에서 날짜와 시간 요약
    • 2.14 환경
      • 2.14.1 attach보다 with 사용
      • 2.14.2 attach 사용
    • 2.15 R 함수 작성
      • 2.15.1 단일표본의 산술평균
      • 2.15.2 단일표본의 중위수
      • 2.15.3 기하평균
      • 2.15.4 조화평균
      • 2.15.5 분산
      • 2.15.6 자유도
      • 2.15.7 분산비 검정
      • 2.15.8 분산 사용
      • 2.15.9 디파싱: 오차 막대에 대한 그래픽 함수
      • 2.15.10 switch 함수
      • 2.15.11 함수의 연산 환경
      • 2.15.12 범위
      • 2.15.13 선택 인자
      • 2.15.14 3개 점 인자의 변수 개수
      • 2.15.15 함수에서 값 반환
      • 2.15.16 무기명 함수
      • 2.15.17 함수에 대한 인자의 유연한 처리
      • 2.15.18 개체의 구조: str
    • 2.16 R에서 파일 작성
      • 2.16.1 작업 내용 저장
      • 2.16.2 이력 저장
      • 2.16.3 그래픽 저장
      • 2.16.4 R에서 생성한 데이터를 디스크에 저장
      • 2.16.5 엑셀 스프레드시트에 붙여넣기
      • 2.16.6 R에서 엑셀이 읽을 수 있는 파일 작성
    • 2.17 프로그래밍 팁

  • 3장 데이터 입력
    • 3.1 키보드에서 데이터 입력
    • 3.2 파일에서 데이터 입력
      • 3.2.1 작업 디렉터리
      • 3.2.2 read.table로 데이터 입력
      • 3.2.3 read.table을 사용하는 경우 일반 오류
      • 3.2.4 구분 기호와 소수점
      • 3.2.5 웹에서 직접 데이터 입력
    • 3.3 scan 함수를 이용해 파일로부터 입력
      • 3.3.1 scan 함수로 데이터 프레임 읽어오기
      • 3.3.2 복잡한 파일 구조에서 scan을 사용해 데이터 입력
    • 3.4 rea dLine s를 사용해 파일에서 데이터 읽어오기
      • 3.4.1 readLines를 사용해 데이터 프레임 입력
      • 3.4.2 readLines를 사용해 비표준 파일 읽기
    • 3.5 데이터 프레임을 atta ch할 때 주의사항
    • 3.6 마스킹
    • 3.7 입출력 포맷
    • 3.8 명령 행에서 파일 확인
    • 3.9 파일에서 날짜와 시간 읽어오기
    • 3.10 내장 데이터 파일
    • 3.11 파일 경로
    • 3.12 연결
    • 3.13 외부 DB에서 데이터 읽어오기
      • 3.13.1 컴퓨터에 적합한 DS N 생성
      • 3.13.2 DB 데이터를 읽기 위한 R 설정

  • 4장 데이터 프레임
    • 4.1 첨자와 지표
    • 4.2 임의로 데이터 프레임에서 행 선택
    • 4.3 데이터 프레임 정렬
    • 4.4 데이터 프레임에서 논리조건으로 행 선택
    • 4.5 누락값 NA를 포함하는 행 생략
      • 4.5.1 NA를 0으로 대체
    • 4.6 인위적 반복을 제거하기 위해 order 와 !dupl icate d 사용
    • 4.7 혼합 순서의 복잡한 정렬
    • 4.8 행 번호 대신 행 이름을 갖는 데이터 프레임
    • 4.9 다른 종류의 개체에서 데이터 프레임 생성
    • 4.10 데이터 프레임에서 중복된 행 제거
    • 4.11 데이터 프레임에서 날짜
    • 4.12 mdatafra mes에서 mat ch 함수 사용
    • 4.13 두 개의 데이터 프레임 병합
    • 4.14 데이터 프레임에 마진 추가
    • 4.15 데이터 프레임의 내용 요약

  • 5장 그래픽스
    • 5.1 이변량 그래프
    • 5.2 2개의 연속형 설명 변수 그래프: 산점도
      • 5.2.1 그래프 기호: pch
      • 5.2.2 그래프의 기호 색상
      • 5.2.3 산점도에 텍스트 추가
      • 5.2.4 산점도에서 개별값 식별
      • 5.2.5 세 번째 변수를 사용해 산점도 라벨링
      • 5.2.6 점 연결
      • 5.2.7 계단식 선 그래프
    • 5.3 그래프에 다른 모양 추가
      • 5.3.1 locator 함수를 사용해 커서로 그래프상에 항목 배치
      • 5.3.2 polygon으로 복잡한 형상 그리기
    • 5.4 수학 함수 그리기
      • 5.4.1 산점도에 부드러운 모수 곡선 추가
      • 5.4.2 산점도를 이용하여 비모수 곡선 적합
    • 5.5 그래픽 창의 모양과 크기
    • 5.6 범주형 설명 변수를 그래프로 표시
      • 5.6.1 유의한 차이를 노치로 표현한 상자그래프
      • 5.6.2 오차막대를 갖는 막대그래프
      • 5.6.3 다양한 비교를 위한 그래프
      • 5.6.4 범주형 설명 변수에 색상 팔레트 사용
    • 5.7 단일 변수 표본 그래프
      • 5.7.1 히스토그램과 막대차트
      • 5.7.2 히스토그램
      • 5.7.3 정수의 히스토그램
      • 5.7.4 히스토그램에 밀도함수 그리기
      • 5.7.5 연속형 변수의 확률밀도 추정
      • 5.7.6 인덱스 그래프
      • 5.7.7 시계열 그래프
      • 5.7.8 파이차트
      • 5.7.9 stripchart 함수
      • 5.7.10 정규성 검증 그래프
    • 5.8 다중 변수를 갖는 그래프
      • 5.8.1 pairs 함수
      • 5.8.2 coplot 함수
      • 5.8.3 교호작용 그래프
    • 5.9 특별한 그래프
      • 5.9.1 설계 그래프
      • 5.9.2 버블 그래프
      • 5.9.3 많은 동일 값을 갖는 그래프
    • 5.10 그래픽을 파일로 저장
    • 5.11 요약

  • 6장 테이블
    • 6.1 데이터 개수 테이블
    • 6.2 요약 테이블
    • 6.3 테이블을 데이터 프레임으로 확장
    • 6.4 데이터 프레임을 테이블로 변환
    • 6.5 prop.table 로 비율 테이블 계산
    • 6.6 scale 함수
    • 6.7 expand.grid 함수
    • 6.8 model.matrix 함수
    • 6.9 table과 tabulate 비교

  • 7장 수학 연산
    • 7.1 수학 함수
      • 7.1.1 로그 함수
      • 7.1.2 3차 곡선 함수
      • 7.1.3 멱함수
      • 7.1.4 다항 함수
      • 7.1.5 감마 함수
      • 7.1.6 비대칭 함수
      • 7.1.7 비대칭 함수의 모수 추정
      • 7.1.8 시그모이드 함수
      • 7.1.9 이항지수 분포 모델
      • 7.1.10 반응 변수와 설명 변수의 변환
    • 7.2 확률 함수
    • 7.3 연속확률 분포
      • 7.3.1 정규 분포
      • 7.3.2 중심극한 이론
      • 7.3.3 정규 분포의 최대우도
      • 7.3.4 평균과 표준편차로 임의의 숫자 생성
      • 7.3.5 데이터의 정규성 비교
      • 7.3.6 가설 검정에 사용된 기타 분포
      • 7.3.7 카이제곱 분포
      • 7.3.8 피셔의 F 분포
      • 7.3.9 스튜던트 t 분포
      • 7.3.10 감마 분포
      • 7.3.11 지수 분포
      • 7.3.12 베타 분포
      • 7.3.13 코시 분포
      • 7.3.14 로그정규 분포
      • 7.3.15 로지스틱 분포
      • 7.3.16 로그로지스틱 분포
      • 7.3.17 와이블 분포
      • 7.3.18 다변량 정규 분포
      • 7.3.19 일양 분포
      • 7.3.20 경험적 누적분포 함수를 그래프로 표시
    • 7.4 이산확률 분포
      • 7.4.1 베르누이 분포
      • 7.4.2 이항 분포
      • 7.4.3 기하 분포
      • 7.4.4 초기하 분포
      • 7.4.5 다항 분포
      • 7.4.6 포아송 분포
      • 7.4.7 음이항 분포
      • 7.4.8 윌콕슨 순위 합 통계
    • 7.5 행렬 대수
      • 7.5.1 행렬곱
      • 7.5.2 대각 행렬
      • 7.5.3 행렬식
      • 7.5.4 역행렬
      • 7.5.5 고유값과 고유벡터
      • 7.5.6 통계 모델에서 행렬
      • 7.5.7 행렬로 통계 모델 표현
    • 7.6 행렬을 사용해 선형 방정식 시스템 문제 해결
    • 7.7 미적분
      • 7.7.1 미분
      • 7.7.2 적분
      • 7.7.3 미분방정식

  • 8장 고전 검사
    • 8.1 단일 표본
      • 8.1.1 데이터 요약
      • 8.1.2 정규성 검정 그래프
      • 8.1.3 정규성 검정
      • 8.1.4 단일 표본 데이터의 사례
    • 8.2 가설 검정에서 부트스트랩
    • 8.3 왜도와 첨도
    • 8.3.1 왜도
      • 8.3.2 첨도
    • 8.4 2개의 표본 검정
      • 8.4.1 2개의 분산비교
      • 8.4.2 두 평균 비교
      • 8.4.3 스튜던트 t 검정
      • 8.4.4 윌콕슨 순위합 검정
    • 8.5 대응표본 검정
    • 8.6 사인 검정
    • 8.7 두 비율을 비교하기 위한 이항 분포 검정
    • 8.8 카이제곱 분할표
      • 8.8.1 피어슨 카이제곱
      • 8.8.2 우발성에 대한 G 검정
      • 8.8.3 귀무가설에서 불균등 확률
      • 8.8.4 테이블 개체에 근거한 카이제곱 검정
      • 8.8.5 작은 기대 빈도를 갖는 분할표: 피셔의 정확 검정
    • 8.9 상관 관계와 공분산
      • 8.9.1 데이터 채취
      • 8.9.2 부분 상관 관계
      • 8.9.3 변수 간 차이에 대한 상관 관계와 분산
      • 8.9.4 척도를 고려한 상관 관계
    • 8.10 콜모고로프 스미르노프 검정
    • 8.11 파워 분석
    • 8.12 부트스트랩
  • 9장 통계 모델링
    • 9.1 선착순
    • 9.2 최대우도
    • 9.3 간결함의 원칙: 오캄의 면도날
    • 9.4 통계 모형 유형
    • 9.5 모형 단순화 단계
      • 9.5.1 주의사항
      • 9.5.2 제거 순서
    • 9.6 R에서 모형 식
      • 9.6.1 설명 변수 사이의 상호작용
      • 9.6.2 수식 개체 생성
    • 9.7 복수 개의 오차 조건
    • 9.8 매개변수 1을 이용한 y 절편
    • 9.9 모형 단순화를 위한 up date 함수
    • 9.10 회귀 분석을 위한 모형 공식
    • 9.11 박스 콕스 변환
    • 9.12 모형 평가
    • 9.13 모형 확인
      • 9.13.1 이분산성
      • 9.13.2 잔차의 비정규성
    • 9.14 영향도
    • 9.15 R에서 통계 모델링의 요약
    • 9.16 모형 적합 함수의 선택인자
      • 9.16.1 부분 집합
      • 9.16.2 중요도
      • 9.16.3 결측값
      • 9.16.4 옵셋
      • 9.16.5 같은 변수명을 포함한 데이터 프레임
    • 9.17 아카이케 정보 기준
      • 9.17.1 모형 적합에 대한 측정값으로서 AIC
    • 9.18 영향력
    • 9.19 오지정 모형
    • 9.20 R에서 모형 체크
    • 9.21 모형 개체에서 정보 추출
      • 9.21.1 이름으로 정보 추출
      • 9.21.2 리스트 첨자로 정보 추출
      • 9.21.3 $를 사용해 모형 성분 추출
      • 9.21.4 모형과 함께 리스트 사용
    • 9.22 연속형과 범주형 설명 변수에 대한 summary 테이블
    • 9.23 대비
      • 9.23.1 대비계수
      • 9.23.2 R에서 대비 분석
      • 9.23.3 사전 대비
    • 9.24 단계 제거에 의한 모형 단순화
    • 9.25 3가지 유형의 대비 비교
      • 9.25.1 실험 조건 대비
      • 9.25.2 헬머트 대비
      • 9.25.3 합 대비
    • 9.26 별칭
    • 9.27 직교 다항 대비: contr .poly
    • 9.28 통계 모델링의 개요

  • 10장 회귀 분석
    • 10.1 선형 회귀
      • 10.1.1 R에서 유명한 값 5개
      • 10.1.2 수정 제곱합과 곱의 합
      • 10.1.3 산점도
      • 10.1.4 분산 분석: SS Y = SS R + SS E
      • 10.1.5 모수에 대한 불신뢰도 추정
      • 10.1.6 적합 모형을 사용해 예측
      • 10.1.7 모형 검사
    • 10.2 기본 함수에 대한 다항 적합
    • 10.3 다항 회귀
    • 10.4 역학 모형을 데이터에 적합
    • 10.5 변환 후 선형 회귀
    • 10.6 회귀식에 의한 예측
    • 10.7 회귀 분석에서 적합도 부족 검정
    • 10.8 회귀식을 이용한 부트스트랩
    • 10.9 회귀식을 이용한 잭나이프
    • 10.10 부트스트랩 후 잭나이프
    • 10.11 잔차에서 시리얼한 상관 관계
    • 10.12 조각별 회귀
    • 10.13 다중 회귀
      • 10.13.1 다중 회귀 모형
      • 10.13.2 다중 회귀 분석에서 발생되는 일반적인 문제

  • 11장 분산 분석
    • 11.1 일원분산 분석
      • 11.1.1 일원 분산 분석 계산
      • 11.1.2 분산 분석의 가정
      • 11.1.3 일원 분산 분석의 예제
      • 11.1.4 효과 크기
      • 11.1.5 일원분산 분석 결과를 해석하기 위한 그래프
    • 11.2 요인 실험
    • 11.3 인위적 반복: 중첩 설계와 분할구
      • 11.3.1 분할구 실험 설계
      • 11.3.2 혼합효과 모형
      • 11.3.3 고정 효과나 랜덤 효과
      • 11.3.4 인위적 반복 제거
      • 11.3.5 파생 변수 분석
    • 11.4 분산성분 분석
    • 11.5 ANOV A에서 효과 크기: aov 또는 lm
    • 11.6 다중 비교
    • 11.7 다변량 분산 분석

  • 12장 공분산 분석
    • 12.1 R에서 공분산 분석
    • 12.2 ANCOV A와 실험 계획
    • 12.3 2개 요인과 1개 연속 공변량을 갖는 ANCOV A
    • 12.4 ANCOV A 모형의 대비와 모수
    • 12.5 summary.aov에서 순서 문제

  • 13장 일반화 선형 모형
    • 13.1 오차 구조
    • 13.2 선형예측 모형
    • 13.3 연결 함수
      • 13.3.1 정준 연결 함수
    • 13.4 비율 데이터와 이항오차
    • 13.5 카운트 데이터와 포아송 오차
    • 13.6 편차: GLM의 적합도 측정
    • 13.7 쿼시우도
    • 13.8 쿼시 모형 부류
    • 13.9 일반화 가법 모형
    • 13.10 옵셋
    • 13.11 잔차
      • 13.11.1 잘못 설정된 오차 구조
      • 13.11.2 잘못 설정된 연결 함수
    • 13.12 과대산포
    • 13.13 GLM을 부트스트랩
    • 13.14 정렬된 범주형 변수를 이용한 이항 GLM

  • 14장 카운트 데이터
    • 14.1 포아송 오차를 갖는 회귀 분석
    • 14.2 카운트 데이터의 편차 분석
    • 14.3 카운트 데이터에 대한 공분산 분석
    • 14.4 빈도 분포
    • 14.5 로그 선형 모형에서 과대 산포
    • 14.6 음이항 오류

  • 15장 테이블 형태의 카운트 데이터
    • 15.1 카운트에 대한 두 클래스 테이블
    • 15.2 카운트 데이터에 대한 표본 크기
    • 15.3 4개 클래스의 카운트 테이블
    • 15.4 2X2 분할표
    • 15.5 단순 분할표를 위한 로그선형 모형 사용
    • 15.6 분할표의 위험
    • 15.7 쿼시포아송과 음이항 모형 비교
    • 15.8 중간 복잡도의 비상 테이블
    • 15.9 S choener 의 도마뱀: 복잡한 분할표
    • 15.10 분할표에 대한 그래프 분석
    • 15.11 카운트 데이터에 대한 그래프: Spin plot과 spinograms

  • 16장 비율 데이터
    • 16.1 한 두 가지의 비율 데이터 분석
    • 16.2 비율에 근거한 카운트 데이터
    • 16.3 배당률
    • 16.4 과대 산포와 가설 검정
    • 16.5 응용
      • 16.5.1 이항 오차를 갖는 로지스틱 회귀 분석
      • 16.5.2 생물학 검정 데이터를 사용해 LD50과 LD90 추정
      • 16.5.3. 범주형 설명 변수에 대한 비율 데이터
    • 16.6 평균 비율
    • 16.7 비율 카운트 데이터를 사용한 모델링 요약
    • 16.8 이항 데이터의 공분산 분석
    • 16.9 복잡한 분할표를 비율 형태로 변환

  • 17장 바이너리 반응 변수
    • 17.1 발생률 함수
    • 17.2 로지스틱 적합의 시각적 검정
    • 17.3 바이너리 반응 변수를 사용한 ANCOV A
    • 17.4 인위적 반복를 갖는 바이너리 반응 변수

  • 18장 일반화 가법 모형
    • 18.1 비모수 평활기
    • 18.2 일반화 가법 모형
      • 18.2.1 기술적 측면
    • 18.3 매우 볼록한 형태의 데이터 예제
    • 18.4 바이너리 데이터를 사용한 일반화 가법 모형
    • 18.5 ga m을 사용해 3차원 그래프 그리기

  • 19장 혼합 모형
    • 19.1 복제와 인위적 반복
    • 19.2 lme 와 lmer 함수
      • 19.2.1 lme
      • 19.2.2 lmer
      • 19.3 최량 선형 불편 예측기
    • 19.4 다른 공간 척도를 사용하도록 설계된 실험: 분할구
    • 19.5 계층적 샘플링 및 분산 요소 분석
    • 19.6 시계열 인위적 반복을 사용한 혼합 모형
    • 19.7 혼합 모형에서 시계열 분석
    • 19.8 설계된 실험에서 랜덤 효과
    • 19.9 혼합 모형에서의 회귀 분석
    • 19.10 일반화 선형 혼합 모형
      • 19.10.1 계층적 구조화된 카운트 데이터

  • 20장 비선형 회귀 분석
    • 20.1 미카엘리스멘텐 방식과 점근지수법 비교
    • 20.2 일반화 가법 모형
    • 20.3 비선형 추정을 위한 그룹화 데이터
    • 20.4 비선형 시계열 모형: 시계열 인위적인 반복
    • 20.5 자동 시작 함수
      • 20.5.1 자동 시작 미카엘리스멘텐 모형
    • 20.5.2 자동 시작 점근지수 모형
    • 20.5.3 자동 시작 로지스틱 모형
    • 20.5.4. 자동 시작하는 4모수 로지스틱 모형
    • 20.5.5 자동 시작 와이블 성장 함수
    • 20.5.6 자동 시작 일차 구획 함수
  • 20.6 비선형 회귀 분석 군의 부트스트랩

  • 21장 메타 분석
    • 21.1 효과 크기
    • 21.2 가중치
    • 21.3 고정 효과와 랜덤 효과
      • 21.3.1 스케일 차에 대한 고정 효과 메타 분석
    • 21.3.2 크기가 조정된 평균차를 이용한 랜덤 효과
    • 21.4 바이너리 데이터의 랜덤 효과 메타 분석

  • 22장 베이지안 통계
    • 22.1 배경
    • 22.2 연속형 반응 변수
    • 22.3 표준 사전 분포와 표준 우도
    • 22.4 사전 확률
      • 22.4.1 공액 사전 분포
    • 22.5 실제로 복잡한 모형을 위한 베이지안 통계
    • 22.6 실제 고려사항
    • 22.7 BUGS 모형 작성
    • 22.8 베이지안 통계를 위한 R 패키지
    • 22.9 JAGS 설치
    • 22.10. R에서 JAGS 실행
    • 22.11 단순 선형 회귀에서 MCMC 사용
    • 22.12 시계열 인위적 반복(pseu dorepl icat ion) 모형에서 MCMC 사용
    • 22.13 이항 오차 모형에서 MCMC 사용

  • 23장 나무 모형
    • 23.1 배경
    • 23.2 회귀 나무
    • 23.3 나무 모형 적합에 rpart 사용
    • 23.4 나무 모형을 회귀 분석으로 사용
    • 23.5 모형 단순화
    • 23.6 범주 설명 변수를 사용한 분류 나무
    • 23.7 복제 데이터를 사용한 분류 나무
    • 23.8 볼록 여부 테스트

  • 24장 시계열 분포
    • 24.1 니콜슨의 검정파리
    • 24.2 이동평균
    • 24.3 계절 데이터
      • 24.3.1 월 평균 내 패턴
    • 24.4 내장 시계열 함수
    • 24.5 분해
    • 24.6 시계열 트렌드 테스트
    • 24.7 스펙트럼 분석
    • 24.8 다중 시계열 분석
    • 24.9 시계열 데이터 시뮬레이션
    • 24.10 시계열 모형

  • 25장 다변량 통계
    • 25.1 주성분 분석
    • 25.2 요인 분석
    • 25.3 군집 분석
      • 25.3.1 분할 방법
      • 25.3.2 kmeans의 분류 사용
    • 25.4 계층적 군집 분석
    • 25.5 판별 분석
    • 25.6 신경망 분석

  • 26장 공간 통계
    • 26.1 점 프로세스
      • 26.1.1 원 안의 임의의 점
    • 26.2 최근접 이웃
      • 26.2.1 테셀레이션
    • 26.3 공간 임의성 검정
      • 26.3.1 리플리의 K
      • 26.3.2 사분면 기반 방법
      • 26.3.3 집합 패턴과 사분면 내 개체수 데이터
      • 26.3.4. 지도에서 카운팅 방법
    • 26.4 공간 통계 패키지
      • 26.4.1 spatstat 패키지
      • 26.4.2 spdep 패키지
      • 26.4.3 다각형 리스트
    • 26.5. 지리통계 데이터
    • 26.6 공간적 수정 오차를 이용한 회귀 모형: 일반화 최소 자승법
    • 26.7 관계형 데이터베이스로부터 점 분포 지도 제작

  • 27장 생존 분석
    • 27.1 몬테 카를로 실험
    • 27.2 배경
    • 27.3 생존 함수
    • 27.4 밀도 함수
    • 27.5. 위험 함수
    • 27.6 지수 분포
      • 27.6.1 밀도 함수
      • 27.6.2 생존 함수
      • 27.6.3 위험 함수
    • 27.7 카플란메이어 생존 분포
    • 27.8 연령별 위험도 모형
    • 27.9 R에서의 생존 분석
      • 27.9.1 모수 모형
      • 27.9.2 콕스 비율 위험도 모형
      • 27.9.3 콕스 비율 위험 모형과 모수 중 더 나은 것
    • 27.10 모수 분석
    • 27.11 콕스 비율 위험도
    • 27.12 중도 절단 모형
      • 27.12.1 모수 모형
      • 27.12.2 coxph와 survreg 생존 분석 비교

  • 28장 시뮬레이션 모형
    • 28.1 시간적 역학 관계: 개체군의 무질서에 대한 역학 관계
      • 28.1.1 무질서 상태가 되는 경로 조사
    • 28.2 시 및 공간 역학 관계: 2차원에서의 랜덤 워크 시뮬레이션
    • 28.3 공간 시뮬레이션 모형
      • 28.3.1 메타 개체군 역학 관계
      • 28.3.2 공간적으로 확실한 (국소) 밀도 의존성에서 발생한 공존 결과
    • 28.4 역학적 교호작용으로 인한 패턴 생성

  • 29장 그래픽 스타일 변경
    • 29.1 출판용 그래프
    • 29.2. 색
      • 29.2.1 색 그룹 팔레트
      • 29.2.2 RColorBrewer 패키지
      • 29.2.3 경계선으로 구분된 기호에 색 설정
      • 29.2.4 범례 색상
      • 29.2.5 배경 색
      • 29.2.6 전면 색
      • 29.2.7 그래프의 부분별로 다른 색과 폰트 사용
      • 29.2.8 그래프의 모든 색 조정
    • 29.3 크로스 해치
    • 29.4 그레이스케일
    • 29.5 다각형에 색 설정
    • 29.6 로그 축
    • 29.7 다양한 텍스트 폰트
    • 29.8 그래프에 수식 및 기호 사용
    • 29.9 위상평면
    • 29.10 굵은 화살표
    • 29.11 3차원 그래프
    • 29.12 wireframe 을 사용한 복잡한 3D 그래프
    • 29.13 알파벳 순서별 그래픽 매개변수 정리
      • 29.13.1 텍스트 자리맞춤, adj
      • 29.13.2 그래프 주석, ann
      • 29.13.3 여러 그래프를 그릴 때 다음 그래프로 넘어가는 것을 늦추는 기능, ask
      • 29.13.4 축 조정, axis
      • 29.13.5 그래프 배경 색, bg
      • 29.13.6 그래프 상자, box
      • 29.13.7 그래프에서 글자 확대 함수를 사용한 기호 크기 조정, cex
      • 29.13.8 그래프 영역 모양 변화, plt
      • 29.13.9 fig를 사용해 불규칙적 레이아웃에 여러 그래프 배치
      • 29.13.10 fig를 사용해 공통 x축 척도에 서로 다른 y축 비율을 사용한 두 그래프 작성
      • 29.13.11 layout 함수
      • 29.13.12 단일 장치에서 여러 화면 생성하고 조정
      • 29.13.13 눈금의 숫자 방향 조정, las
      • 29.13.14 선의 끝 모양 조정과 선 연결하기, lend와 ljoin
      • 29.13.15 선 모양, lty
      • 29.13.16 선 두께, lwd
      • 29.13.17 동일한 화면에 여러 그래프 그리기, mfrow와 mfcol
      • 29.13.18 그래프 주변에 여백 넣기, mar
      • 29.13.19 같은 축에 1개 이상의 그래프 그리기, new
      • 29.13.20 동일한 그래프 화면에 서로 다른 y축을 갖는 두 그래프 작성
      • 29.13.21 외부 여백, oma
      • 29.13.22 그래프 모아 보기
      • 29.13.23 정사각형 그래프 영역, pty
      • 29.13.24 글자 회전, srt
      • 29.13.25 축 라벨 회전
      • 29.13.26 축의 눈금 표시
      • 29.13.27 축 유형
    • 29.14 트렐리스 그래픽
      • 29.14.1 상자수염 그래프 패널
      • 29.14.2 산점도 패널
      • 29.14.3 막대 그래프 패널
    • 29.14.4 조건 그래프 패널
    • 29.14.5 히스토그램 패널
    • 29.14.6 효과 크기

    • 도서 오류 신고

    도서 오류 신고

    에이콘출판사에 관심을 가져 주셔서 고맙습니다. 도서의 오탈자 정보를 알려주시면 다음 개정판 인쇄 시 반영하겠습니다.

    오탈자 정보는 다음과 같이 입력해 주시면 됩니다.

    (예시) p.100 아래에서 3행 : '몇일'동안 -> 며칠동안

    정오표

    정오표

    [ p76 7~31행 ]

    [ p410 1행 ]

    det A=0 -> det A≠0

    [ p410 3행, 5행 ]

    |A| = 0 -> |A| ≠ 0

    [ p482 하단의 역자주 ]

    실재론과 대린하는 철학적 입장이며, 유명론이라고도 부른다. 명목론에서는 실재하는 것을 '개체'와 개체이 붙인 '이름'뿐이라고 본다. -> 실재론과 대립하는 철학적 입장이며, 유명론이라고도 부른다. 명목론에서는 실재하는 것을 '개체'와 개체에 붙인 '이름'뿐이라고 본다.

    [ p610 하단부 ]

    fligner.test(y~soile) -> fligner.test(yield~soile)

    bartlett(y~soil) -> bartlett(yield~soil)

    [p.140 : 5행]
    개별 문자열은 각각 3, 3, 6, 7개의 문자를
    ->
    개별 문자열은 각각 3, 3, 6, 8개의 문자를

    [p.150 : 아래에서 8행]

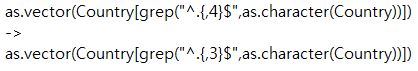
    [p.201 : 아래에서 11행]
    data<-read.table(yield.txt",header=T)
    →
    data<-read.table("yield.txt",header=T)

    [p.202 : 3행]
    data<-rt("yields")
    data<-rt("yield")

    [p.218 : 3.12 연결 9행]
    사용될 수 있도록 있다.
    ->
    사용될 수 있다.

    [p.265 : 4행]
    col=c(“red”,“blud”)
    ->
    col=c(“red”,“blue”)

    [p.885 : 아래서 2행]
    영향을 더 많은
    ->
    영향을 더 많이

    [p.1006 : 4행]
    1981년 넌문
    ->
    1981년 논문

    [p.1037 : 아래서 10행]
    임의위 수가
    ->
    임의의 수가

    [ p828, 830, 854, 920, 937, 938, 1128 ]

    자동 회귀 -> 자기 회귀

    [ p588, 630, 853, 854, 917, 919, 920, 921, 926, 927, 932, 934, 936, 937, 938, 939, 992, 993, 1126, 1128 ]

    자동 상관 -> 자기 상관

    부분 자동 상관 -> 부분 자기 상관