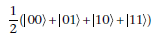책 소개
2021년 대한민국학술원 우수학술도서 선정도서
'양자 컴퓨터 원리와 수학적 기초' 유튜브 영상입니다.
요약
기본적인 수학 배경지식을 갖춘 독자를 대상으로 양자 컴퓨터의 기본 원리를 설명하는 이론서다. 얽힘, 중첩 등 양자 컴퓨터의 바탕이 되는 양자역학적 개념의 수학적 모델을 가급적 단순화해서 설명하므로, 고등학교 수준의 수학 지식이 있으면 내용을 따라갈 수 있다. 양자 컴퓨터의 수학적 기초를 쌓고자 하는 독자에게 좋은 입문서 혹은 보조 교재다.
추천의 글
“최근 들어 언론이 양자 컴퓨팅 혁명이 도래한 것에 관해 수많은 기사를 쏟아내고 있습니다. 이 책의 저자인 크리스 베른하트는 매력적인 양자 컴퓨팅 분야에 관심 있는 모든 이에게 기초를 가르칠 수 있는 책을 놀랄 만한 솜씨로 간결하게 완성했습니다. 독자들은 고등학교 수준의 수학만 알고 있으면 됩니다. 그러면 양자 컴퓨터의 많은 부분으로 아주 친절한 안내를 받게 될 것입니다.”
- 노손 S. 야노프스키(Noson S. Yanofsky)/ 브루클린대학교 컴퓨터 및 정보과학과 교수, 『Quantum Computing for Computer Scientists』 공동 저자이자 『The Outer Limits of Reason』 저자
“베른하트는 양자 컴퓨팅에 관한 명료하고 정확한 개론서를 썼습니다. 초심자는 이 책을 읽고 양자 순간이동, 벨의 부등식, 사이먼의 알고리즘 등을 제대로 이해할 수 있습니다. 초심자가 나에게 적당한 양자 컴퓨팅 책을 묻는다면, 단연 이 책을 추천할 것입니다”
- 스콧 애론슨(Scott Aaronson)/ 텍사스대학교 데이비드 제이 브루톤 센테니얼 컴퓨터과학과 교수이자 양자정보센터 디렉터, 『Quantum Computing since Democritus』 저자
“비트는 큐비트로 대체될 것인가? 양자 컴퓨터는 기술의 수평선에서 떠오르고 있습니다. 이 책은 IT 리더들이 양자 효과를 구경하기만 하는 것을 넘어 양자 컴퓨팅의 기초에 도달하는 길을 터줍니다.”
- 알렉산더 키와틴 듀드니(Alexander Keewatin Dewdney)/ 웨스턴온타리오대학교 컴퓨터과학 교수
이 책의 대상 독자
이 책의 목적은 고등학생 수준의 수학에 익숙한 독자에게 양자 컴퓨팅을 소개하는 것이다. 특히 큐비트, 얽힘, 양자 순간 이동, 주요 양자 알고리즘을 공부하며 각 개념을 모호하게 아는 데 그치지 않고 명확하게 이해하는 것을 목표로 한다.
이 책의 구성
1장. 스핀
고전적인 컴퓨팅의 기본 단위는 비트다. 비트는 2개의 상태 중에서 하나의 상태를 가질 수 있는 것이라면 무엇으로든 표현될 수 있다. 가장 흔한 예가 on 또는 off 상태일 수 있는 전기 스위치다. 양자 컴퓨팅의 기본 단위는 ‘큐비트’다. 큐비트는 전자의 스핀 또는 광자의 편광으로 표현될 수 있다. 하지만 스핀과 편광의 성질은 on 또는 off 상태일 수 있는 스위치만큼 우리에게 친숙하지 않다.
우리는 원자의 자기적 성질을 연구했던 오토 슈테른(Otto Stern)과 발터 게를라흐(Walther Gerlach)의 실험을 시작으로 스핀의 기본 특성을 알아볼 것이다. 다양한 방향에서 스핀을 측정할 때 무슨 일이 일어나는지 살펴보고, 측정 행위가 큐비트의 상태에 영향을 줄 수 있음을 배운다. 측정에는 본질적인 무작위성이 관련돼 있음도 설명할 것이다. 그리고 편광 필터와 빛을 사용해 전자 스핀 실험과 유사한 실험을 할 수 있음을 보여주면서 1장을 마무리한다.
2장. 선형대수학
양자 컴퓨팅은 선형대수학이라고 부르는 수학을 바탕으로 한다. 다행히 그 가운데 몇 개의 개념만 알아도 된다. 독자에게 필요한 선형대수학을 소개하고, 이 책에서 어떻게 사용할 것인지 예제를 통해 보여준다.
벡터와 행렬을 소개한 뒤 벡터의 길이를 계산하는 방법, 2개의 벡터가 서로 수직인지 여부를 판단하는 방법을 선보인다. 처음에는 벡터의 기초 연산만 고려하지만, 행렬을 사용함으로써 다수의 벡터 연산을 동시에 계산할 수 있는 단순한 방법을 보여줄 것이다.
2장의 내용을 처음 배울 때는 선형대수학 공부가 얼마나 쓸모 있을지 느끼기 어려울 수 있다. 하지만 선형대수학은 정말로 유용하다. 양자 컴퓨팅의 토대를 형성하기 때문이다. 3장 이후의 내용은 2장에서 소개한 수학을 사용하므로 2장을 주의 깊게 읽어둬야 한다.
3장. 스핀과 큐비트
1장과 2장의 내용이 어떻게 연결되는지 3장에서 볼 수 있다. 스핀 또는 편광의 수학적 모형이 선형대수학으로 주어질 것이다. 우리는 이를 통해서 큐비트를 정의하고, 큐비트를 측정할 때 무슨 일이 일어나는지 설명할 수 있다.
다양한 방향에서 큐비트를 측정하는 예제가 제시된다. 그런 다음 BB84 프로토콜이라는 양자 암호화에 대한 소개로 3장을 마무리한다.
4장. 얽힘
2개의 큐비트가 서로 얽힌다는 것의 의미가 무엇인지 설명한다. 얽힘은 말로 설명하기 어렵지만 수학적으로는 쉽게 표현할 수 있다. 또한 새로운 수학 개념인 텐서곱을 소개한다. 텐서곱은 개별 큐비트의 수학적 모형을 결합해 큐비트의 집합을 기술하는 1개의 모형을 제공하기 위한 가장 단순한 방법이다.
얽힘은 수학적으로 간단히 나타낼 수는 있지만 우리가 일상생활에서 경험할 수 없는 현상이다. 서로 얽힌 큐비트 중 하나를 측정하면, 다른 큐비트가 영향을 받는다. 이것은 과학자 아인슈타인이 “도깨비 같은 원격 작용”이라고 불렀던 현상이다. 이에 관한 몇 가지 예제를 살펴볼 것이다. 얽힘을 사용해 빛보다 빠른 속도의 통신을 구현할 수는 없음을 보여주는 것으로 4장을 마무리한다.
5장. 벨의 부등식
얽힘에 관한 아인슈타인의 관심을 살펴보고, 숨은 변수 이론이 국소적 실재론을 지킬 수 있을지 알아본다. 벨의 부등식을 수학적으로 검토하는데, 이 식을 사용하면 아인슈타인 주장의 정당성을 실험적으로 판단할 수 있다. 훗날 아인슈타인의 주장은 틀린 것으로 드러났다. 하지만 벨조차도 아인슈타인이 옳다고 증명될 것이라 생각했었다.
아르투르 에커트(Artur Ekert)는 벨의 부등식을 검증하는 실험이 암호화를 위한 키 생성 및 도청자 확인 용도로 쓰일 수 있음을 알았다. 이 암호화 프로토콜에 관한 설명으로 5장을 마무리한다.
6장. 고전적 논리, 게이트, 회로
우선 컴퓨팅의 기본 주제인 비트, 게이트, 논리를 설명하고, 가역적 컴퓨팅과 에드 프레드킨(Ed Fredkin)의 아이디어를 간단히 살펴볼 것이다. 또, 프레드킨 게이트와 토폴리 게이트가 범용 게이트임을 증명한다. 다시 말해 프레드킨 게이트(혹은 토폴리 게이트)만을 사용해서 완전한 컴퓨터를 제작할 수 있다. 끝으로, 프레드킨의 당구공 컴퓨터를 소개한다. 당구공 컴퓨터는 이 책의 주제와 직접 관련되지는 않지만, 매우 독창적인 개념이기에 이 책에 포함했다.
당구공 컴퓨터는 벽에 부딪히고 서로 충돌하는 공으로 구성된다. 상호작용하는 입자들의 이미지를 떠올리면 된다. 또한 리처드 파인만이 양자 컴퓨터에 흥미를 갖게 만든 개념 중 하나이기도 하다. 파인만은 당구공 컴퓨터에 관한 초기 논문을 작성했다.
7장. 양자 게이트와 양자 회로
양자 회로를 사용해 양자 컴퓨팅을 알아보는 것으로 시작한다. 먼저, 양자 게이트를 정의한다. 그리고 양자 게이트가 큐비트에 어떻게 작용하는지 살펴보고, 사실은 양자 게이트의 개념을 이미 사용해왔음을 알게 된다. 단지 관점의 차이일 뿐이다. 직교행렬이 측정 장치가 아니라 큐비트에 대해 작용한다고 생각하는 것이다. 초고밀도 코딩, 양자 순간 이동, 복제, 에러 정정에 관한 놀라운 결과들을 증명한다.
8장. 양자 알고리즘
아마도 가장 어려운 장일 것이다. 몇 개의 양자 알고리즘을 살펴보고 이 알고리즘들이 고전적 알고리즘에 비해 얼마나 빨리 계산할 수 있는지 보여준다. 알고리즘의 속도를 논의하기 위해서는 복잡도 이론의 개념을 소개할 필요가 있다. 먼저 쿼리 복잡도(query complexity)를 정의한 뒤, 3개의 양자 알고리즘을 소개하고 이 알고리즘들이 쿼리 복잡도의 관점에서 고전적 알고리즘보다 얼마나 빠른지 보여준다.
양자 알고리즘은 해결하고자 하는 문제의 근본에 존재하는 구조를 파고든다. 단순히 양자 병렬성, 즉 입력값들을 모든 가능한 상태들의 중첩으로 만들 수 있음을 이용하는 것이 아니다. 이 책에서 소개하는 수학적 도구들의 마지막으로 행렬의 크로네커곱을 소개한다. 8장의 내용이 어려운 것은 새로운 수학적 도구가 도입되기 때문이 아니라, 우리가 완전히 새로운 방법으로 계산하고 있으며 이런 새로운 개념을 사용해 문제를 푼 경험이 없다는 사실 때문이다.
9장. 양자 컴퓨팅의 영향력
마지막 장인 9장은 양자 컴퓨팅이 우리의 삶에 미칠 영향을 살펴본다. 먼저 피터 쇼어(Peter Shor)와 로브 그로버(Lov Grover)가 고안한 2개의 중요한 알고리즘을 간단히 설명한다. 각각의 알고리즘 소개를 끝낸 뒤, 양자 컴퓨팅이 양자적 프로세스를 시뮬레이션하는 데 어떻게 사용될 수 있는지 알아본다. 화학의 근본 바탕은 양자역학이다. 고전적인 전산화학은 양자역학 방정식을 고전적 컴퓨터를 사용해 시뮬레이션하고 있지만, 시뮬레이션은 근삿값일 뿐이며 세부 사항이 무시되곤 했다. 대체로 근삿값만으로 충분하지만, 어떤 경우에는 세부 사항이 고려돼야 하는데, 이때 양자 컴퓨터가 해결책을 제시할 수 있다.
9장은 실제 양자 컴퓨터의 제작에 관해서도 간단히 소개한다. 이 분야는 매우 빠르게 발전하고 있다. 이미 시중에 판매 중인 기계도 있다. 또, 모든 사람이 사용할 수 있도록 클라우드에서 서비스되는 것도 있다. 우리는 조만간 양자 우위(quantum supremacy)의 시대에 접어들 가능성이 높다.
마지막으로 양자 컴퓨팅이 새로운 유형의 컴퓨팅이 아니며 컴퓨팅의 진정한 본질에 대한 발견이라는 깨달음으로 이 책을 마무리한다.
목차
목차
- 1장. 스핀
- 양자 시계
- 동일 방향으로 반복 측정
- 서로 다른 방향으로 반복 측정
- 측정
- 무작위성
- 광자와 편광
- 결론
- 2장. 선형대수학
- 복소수 대 실수
- 벡터
- 벡터의 다이어그램
- 벡터의 길이
- 실수배(혹은 스칼라 곱셈)
- 벡터 덧셈
- 직교 벡터
- 브라에 켓 곱하기
- 브라켓과 길이
- 브라켓과 직교
- 정규직교 기저
- 기저 벡터들의 선형 조합으로서의 벡터
- 순서 기저
- 벡터의 길이
- 행렬
- 행렬 계산
- 직교행렬과 유니타리행렬
- 선형대수학 도구 상자
- 3장. 스핀과 큐비트
- 확률
- 양자 스핀을 위한 수학
- 동치 상태 벡터
- 특정 스핀 방향의 기저
- 608만큼 장치 회전
- 광자 편광을 위한 수학 모델
- 특정 편광 방향의 기저
- 편광 필터 실험
- 큐비트
- 앨리스, 밥, 이브
- 확률 진폭과 간섭
- 앨리스, 밥, 이브 그리고 BB84 프로토콜
- 4장. 얽힘
- 앨리스와 밥의 큐비트가 서로 얽혀 있지 않은 경우
- 큐비트가 얽히지 않은 경우
- 큐비트가 얽혀 있는 경우
- 초광속 통신
- 텐서곱의 표준 기저
- 큐비트를 얽는 방법
- CNOT 게이트를 사용해 큐비트 얽기
- 얽힌 양자 시계
- 5장. 벨의 부등식
- 다른 기저로 얽힌 큐비트 측정
- 아인슈타인과 국소적 실재론
- 아인슈타인과 숨은 변수
- 얽힘에 대한 고전 물리학적 설명
- 벨의 부등식
- 양자역학의 답
- 고전적 모델의 답
- 측정
- 양자 키 배포를 위한 에커트 프로토콜
- 6장. 고전적 논리, 게이트, 회로
- 논리
- 부울 대수
- 함수 완전성
- 게이트
- 회로
- NAND는 범용 게이트다
- 게이트와 컴퓨팅
- 메모리
- 가역 컴퓨팅
- 당구공 컴퓨팅
- 7장. 양자 게이트와 양자 회로
- 큐비트
- CNOT 게이트
- 양자 게이트
- 1개의 큐비트에 대해서 동작하는 양자 게이트
- 아마다르 게이트
- 범용 양자 게이트가 존재하는가?
- 복제 불가 정리
- 양자 컴퓨팅 대 고전적 컴퓨팅
- 벨 회로
- 초고밀도 코딩
- 양자 순간 이동
- 오류 정정
- 8장. 양자 알고리즘
- 복잡도 클래스 P와 NP
- 양자 알고리즘은 고전적 알고리즘보다 빠른가?
- 쿼리 복잡도
- 도이치 알고리즘
- 하다마드 행렬의 크로네커곱
- 도이치-조사 알고리즘
- 사이먼의 알고리즘
- 복잡도 클래스
- 양자 알고리즘
- 9장. 양자 컴퓨팅의 영향력
- 쇼어 알고리즘과 암호 해석
- 그로버의 알고리즘과 데이터 검색
- 화학 및 시뮬레이션
- 하드웨어
- 양자 우위와 평행 우주
- 컴퓨팅
관련 블로그 글
지식 충전, 감성 회복! 에이콘출판사와 함께하는 여름휴가 추천 도서 12
반년 넘게 달려온 바쁜 일상 속에서 잠시 숨을 고르고, 나만의 시간과 공간을 되찾을 수 있는 소중한 휴식의 계절입니다. 누구는 바다로, 누구는 산으로 떠나지만, 어떤 이는 책 속으로 떠나는 여행을 택합니다. 단순한 쉼을 넘어, 생각의 지평을 넓히고 나를 되돌아보는 시간. 여름 휴가를 맞아, 일상에서 잠시 벗어나 지식과 성찰, 기술과 통찰을 동시에 얻을 수 있는 책 12권을 소개합니다.
▶ 기술과 지식의 근육을 단련하는 책
◆ Kotlin in Action: 2/e
개발자가 가장 주목해야 할 언어 중 하나인 ‘코틀린’을 가장 체계적으로 설명한 책.
개정 2판에서는
코루틴, 함수형 프로그래밍, 모던 문법 등이 풍부하게 추가되어
있어 초보자부터 숙련자까지 모두에게 가치 있는 지침서다. 여유로운 휴가 기간 동안
천천히 코드를 따라가며, ‘더 나은 코드’를 쓰는 감각을
키우기에 최적이다.
◆ 자바 ORM 표준 JPA 프로그래밍
JPA의 개념과 원리, 실무 적용까지 한 권에 담은, 자바 개발자들의 바이블.
일상에서는 해결책만 급히 찾기 바빴다면, 휴가 중에는
ORM과 영속성 컨텍스트, 엔티티 매핑에 대해 개념부터 다시 탄탄히 쌓아보자. 복잡했던 퍼즐이 조각처럼 맞춰지는 쾌감을 느낄 수 있다.
◆ 개발자를 위한 레디스
레디스를 ‘왜’, ‘어떻게’ 쓰는지를 깊이 있게 짚어주는 실용서.
단순한 캐시 서버가 아닌, 고성능 데이터 처리의 핵심 도구로서 레디스를 제대로 이해하고 싶은 개발자에게 이상적이다. 평소에는 미뤄뒀던 큐 시스템, Pub/Sub, 세션 관리 등을 체계적으로
정리해볼 수 있는 절호의 타이밍.
▶ 수학과 물리, 복잡계 속 세계를 탐험하는 책
◆ 비선형 동역학과 카오스(2판)
카오스 이론과 복잡계 시스템을 본격적으로 다룬 정통 교재.
수식과 그래프, 실험을 통해 ‘예측 불가능함’ 속의 질서를 탐색한다. 긴 호흡이 필요한 책이지만, 여름 휴가는 오히려 그런 책과 만나기 딱 좋은 시간이다. 사고의
지평을 확장시켜줄 묵직한 과학 독서의 동반자.
◆ 양자 컴퓨터 원리와 수학적 기초
양자 컴퓨팅의 이론과 수학을 논리적으로 설명한 입문서.
추상적 개념들이 기초 수학과 연결되며, ‘양자’라는
미지의 세계가 조금씩 눈앞에 모습을 드러낸다. 딥러닝, 물리, 정보이론에 관심 있는 독자에게는 한 여름의 지적 오디세이가 될 것이다.
▶ 창작과 기획의
영감을 얻고 싶은 이들을 위한 책
◆ 게임 시나리오 기획자를 위한 안내서
스토리텔링과 인터랙션 설계, 캐릭터와 세계관 창작의 실무를 총망라한
실전 가이드.
게임을 좋아하는 사람이라면, 이 책은 게임을 ‘만드는
쪽’의 사고로 세계를 바라보는 기회를 제공한다. 창작에 대한
막연한 열망을 구체적인 언어와 기획 프레임으로 풀어낼 수 있도록 돕는다.
▶ 기술이 만든 세상, 그 안의 인간을 고민하는 책
◆ 미래를 바꾼 아홉 가지 알고리즘
우리 삶
깊숙이 들어온 알고리즘을 알고 싶다면 이 책이 출발점이다.
검색, 암호화, 오류 수정 등 일상 속 기술
뒤에 숨은 수학과 컴퓨터 과학의 원리를 쉽게 풀어낸다. 가볍게 읽히면서도, ‘기술이 세상을 어떻게 바꾸는가’를 곱씹게 하는 흥미로운 과학 교양서.
◆ 두 얼굴의 신기술: AI 딜레마
AI 시대의 윤리, 책임, 인간성에 대한 근본적인 질문을 던지는 책.
기술은 진보하지만, 인간의 선택은 늘 복잡하다. 이
책은 AI 기술을 둘러싼 양면성을 풍부한 사례와 질문으로 풀어내며, 여름이라는
여유 속에서 사유와 토론의 기회를 제공한다.
▶ 스스로를
돌아보고, 세상을 다시 바라보는 인문·사회서
◆ 오늘도 견뎌온 당신에게
지친 이들을 위한 진심의 언어가 담긴 심리 에세이.
견디는 것이 전부인 날들 속에서, ‘그럼에도’ 살아내고 있는 우리에게 조용히 말을 건넨다. 혼자 있는 시간, 혼자여서 더 고마운 말이 되어줄 것이다.
◆ 삶은 속도가 아니라 방향이다
빠름이 미덕처럼 여겨지는 세상에서 ‘방향’을 말하는 책.
저자는 느림의 미학을 통해 자신을 더 깊이 들여다보는 법을 이야기한다. 특히 바쁜 일상 속에서
놓쳤던 삶의 균형을, 여름의 틈에서 되찾고 싶은 이들에게 추천한다.
◆ 인생은 내리막길에서 훨씬 성숙해진다
내리막이라
여긴 시간들 속에서 오히려 성숙과 성찰이 시작된다는 담담한 고백.
중년 이후의 삶을 새롭게 받아들이는 철학적이고 따뜻한 시선이 담겨 있다. 휴가지에서
마음을 가만히 내려놓고 읽기에 더없이 좋은 동반서.
▶ 지정학과 경제 전쟁, 세계를 읽는 전략서
◆ 지경학의 부활
지정학과 경제 안보의 교차점을 다룬 본격 지식서.
미국과 중국의 패권 경쟁, 제재 정책, 반도체 산업까지, 복잡한 국제 질서를 해석하는 ‘지경학’의 시선을 제시한다. 글로벌 정세에 관심 있는 독자라면, 여름이 지나기 전 꼭 읽어볼 만한 책이다.
이 책들은
평소 몰입하기 어려운 주제나, 깊은 사고가 필요한 내용을 담고 있어,
‘시간의 여유’가 있는 여름 휴가에 특히 잘 어울립니다.
특히 지금의 나를 돌아보고, 다음 스텝을 준비하는 데 매우 유용합니다.
12권의 책과 함께 지식은 쌓고, 마음은 가벼워지는 여름 되시길 바랍니다.
크리에이티브 커먼즈 라이센스 이 저작물은 크리에이티브 커먼즈 코리아 저작자표시 2.0 대한민국 라이센스에 따라 이용하실 수 있습니다.
도서 오류 신고
정오표
정오표
[p.28 : 그림 1.3]
수평 방향으로 스핀 S인 전자
->
수직 방향으로 스핀 S인 전자
[p.30 : 2행]
기술하는 빙밥은
->
기술하는 방법은
[p.30 : 아래서 8행]
그레서 바늘이
->
그래서 바늘이
[p.34 : 3행]
대상이 되는 상호작용 해야 하며,
->
대상이 되는 입자와 상호작용 해야 하며,
[p.54 : 1행]
x2 = <|b2> | v>
->
x2 = <b2 | v>
[p.76 : 13행]
따라서 큐비트
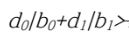 을 측정하면,
을 측정하면,
->
따라서 큐비트
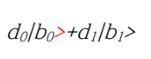 을 측정하면,
을 측정하면,
[p.77 : 9행]
따라서
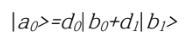 형태로 쓸 수 있다
형태로 쓸 수 있다
->
따라서
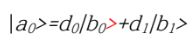 형태로 쓸 수 있다
형태로 쓸 수 있다
[p.128 : 아래에서 2행]
표시돼 있다. 이므로
->
표시돼 있다.
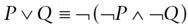 이므로
이므로
[p.129 : 그림 6.8]

->
[p.135 : CNOT 진리표 1행 4열]
1
->
0
[p.149 : 첫 번째 CNOT 표 x⊕y 1행]
1
->
0
[p.149 : 두 번째 CNOT 표 x⊕y 1행]
1
->
0
[p.170 : 회로도 그림 좌측 상단]
ǀ0> + bǀ1>
->
aǀ0> + bǀ1>
[p.182 3,4 행]
f1(0)=0 -> f1(1)=1
f2(0)=0 -> f2(1)=0
[p.195 : 3행]
열 00과 01을
->
열 00과 10을
[p.214 : 7행 아래]